理想的な弦ではなく、理想的な長い板を叩いたときの周波数比に由来する「12.3音平均律」
概要
12音平均律というのは、理想的な弦の振動による周波数比が 1 : 2 : 3 : 4 : 5 : 6 : ... となることと、$2^{7/12} = 1.4983\dots \approx \frac{3}{2}$ および $2^{4/12} = 1.2599\dots \approx \frac{5}{4}$ であることに由来する。完全八度を12分割して得られる代物を共通尺度にすることで、そいつを7つ集めて純正完全五度っぽいものが、そいつを4つ集めて純正長三度っぽいものが再現できてうれしい、というのが12音平均律の根拠である。
さて、では「理想的な弦の振動」ではなくて「理想的な長い板の振動」ならどうであろうか。あ、今回は自由端だけ扱うこととする。
結論を先に言うと、周波数比は 3.0112² : 4.9995² : 7² : 9² : ... になる。この周波数比に言及している文献はわりとあったが、導出してるやつがなかなか見つからずに私が苦労したのでまずはこれの導出をしてから、「12.3音平均律」の提唱に移りたい。
周波数比の導出
微分方程式
オイラー・ベルヌーイの梁理論というやつを使うと、長さ $L$ の梁が材料においても断面の形においても一様である場合、たわみ $w(x, t)$ ($x$ は梁の伸びている方向に沿って定義された座標)の挙動を表す微分方程式は
$$EI\frac{\partial^4 w}{\partial x^4} = \left(- \frac{\partial^2 w}{\partial t^2} \right)\rho A$$
と書ける。ここで $\rho$ [kg/m³] は素材の密度、$A$ [m²] は梁の断面積。$EI$ [N・m²] は曲げ剛性と言われる量であり、材質により決まる弾性率 $E$ [Pa] と、断面の形によって決まる量である面積の第二モーメント $I$ [m⁴] を掛け合わせたものであるらしい。重力加速度は無視したが、欲しい場合はカッコでくくった $- \frac{\partial^2 w}{\partial t^2} $ の項にさらに重力加速度を足せばいい。
境界条件
さて、二階微分というのは曲線が局所的にどれくらい強く曲がっているかを表すわけで、たわみの $x$ についての二階微分 $\frac{\partial^2 w}{\partial x^2}$ は両端 $x=0$ と $x=L$ でゼロになる。
自由端なので、両端での剪断応力もゼロになる。したがってたわみの $x$ についての三階微分も両端でゼロである。
方程式を解く
$$\left(EI\frac{\partial^4 }{\partial x^4} + \rho A \frac{\partial^2 }{\partial t^2}\right) w = 0$$
を解くために、まず $w(x,t) = X(x)T(t)$ という形の解を仮定して
$$\frac{EI}{\rho A} \frac{1}{X}\frac{d^4 X}{d x^4} = - \frac{1}{T}\frac{d^2 T}{d t^2}$$
どうせ $T$ は角振動数 $\omega$ の三角関数で、したがって $\frac{EI}{\rho A} \frac{1}{X}\frac{d^4 X}{d x^4} = \omega^2$ となればよい。 $k = \left(\frac{\rho A \omega^2}{EI}\right)^{1/4}$ と置いて $\frac{d^4 X}{d x^4} = k^4X$ と書いてやれば、
$$X = \alpha \mathrm{cos h}(kx) + \beta \mathrm{sin h}(kx) + \gamma \cos(kx) + \delta \sin(kx)$$
になることがすぐにわかる。さて境界条件。
$X'' = k^2 (\alpha \mathrm{cos h}(kx) + \beta \mathrm{sin h}(kx) - \gamma \cos(kx) - \delta \sin(kx))$ と $X''' = k^3 (\alpha \mathrm{sin h}(kx) + \beta \mathrm{cos h}(kx) + \gamma \sin(kx) - \delta \cos(kx))$ が $x=0$ と $x=L$ の両端でゼロになる必要があるので、
$$\begin{pmatrix}1 & 0 & -1 & 0 \\ \mathrm{cos h} kL & \mathrm{sin h} kL & -\cos kL & -\sin kL \\ 0 & 1 & 0 & -1 \\ \mathrm{sin h} kL & \mathrm{cos h} kL & \sin kL & -\cos kL \end{pmatrix} \begin{pmatrix}\alpha \\ \beta \\ \gamma \\ \delta \end{pmatrix} = \begin{pmatrix}0 \\ 0 \\ 0 \\ 0\end{pmatrix}$$
第一行と第三行(つまり $x=0$ での境界条件)を見ると $\alpha = \gamma$ と $\beta = \delta$ が分かるので、
$$\begin{pmatrix} \mathrm{cos h} kL -\cos kL& \mathrm{sin h} kL -\sin kL \\ \mathrm{sin h} kL + \sin kL & \mathrm{cos h} kL - \cos kL \end{pmatrix}\begin{pmatrix}\alpha \\ \beta \end{pmatrix} = \begin{pmatrix}0 \\ 0 \end{pmatrix}$$
ここで
$$\begin{align*} \det \begin{pmatrix} \mathrm{cos h} kL -\cos kL& \mathrm{sin h} kL -\sin kL \\ \mathrm{sin h} kL + \sin kL & \mathrm{cos h} kL - \cos kL \end{pmatrix} &= ( \mathrm{cos h} kL -\cos kL )^2 - (\mathrm{sin h} kL - \sin kL)(\mathrm{sin h} kL + \sin kL)\\
&= \cos^2 kL - 2\cos kL \mathrm{cos h} kL + \mathrm{cos h}^2 kL - \mathrm{sin h}^2 kL + \sin^2 kL \\
&= 2 - 2\cos kL \mathrm{cos h} kL\end{align*}$$
であることに着目すると、$\cos kL \ \mathrm{cos h} kL - 1 = 0$ でない限り先ほどの方程式に非自明解が存在するはずがない。
これをプロットしてみると、
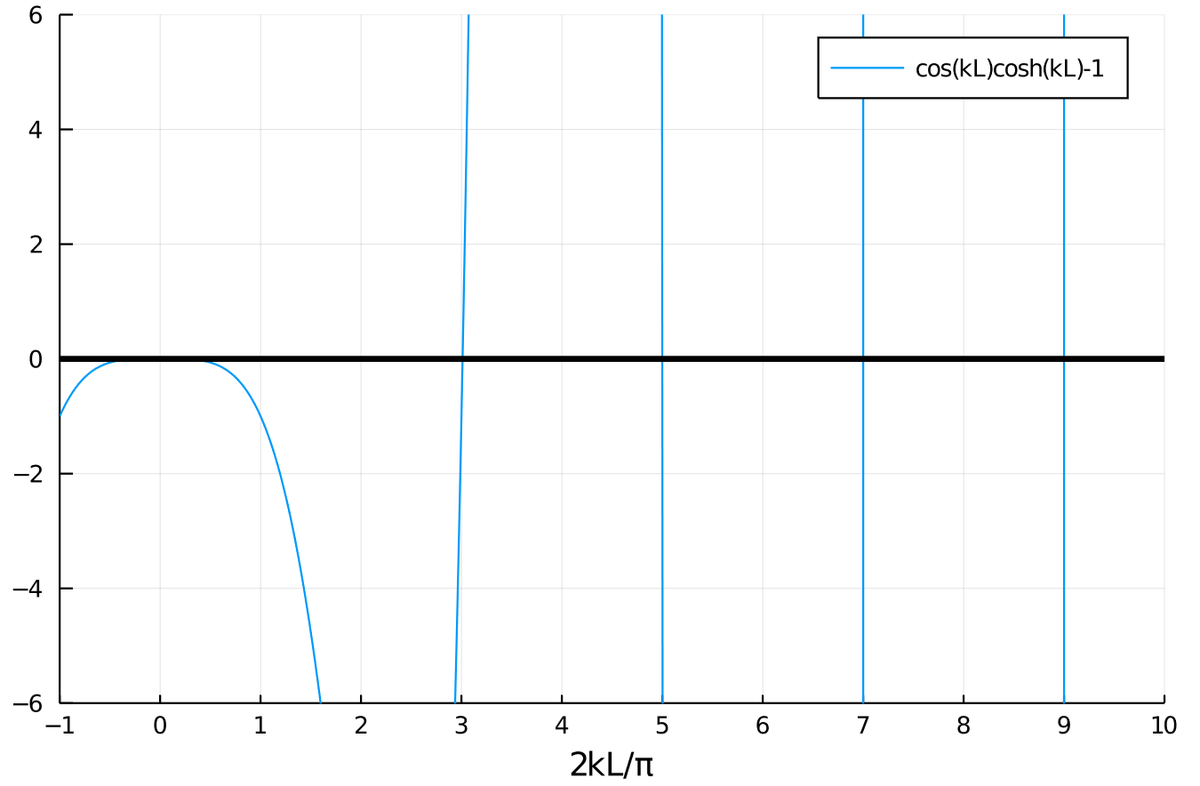
お、3 : 5 : 7 : 9 の謎が見えてきた。
近似
ということで、 $\frac{2kL}{\pi}$ は $3, 5, 7, \dots$ にかなり近いっぽいので、これを評価するために $a_n$ を$1 = \cos(\pi a/2)\ \mathrm{cos h}(\pi a/2)$ の $n$番目の正の解とすると、グラフから $\epsilon_n = a_n - (2n+1)$ が非常に小さい値であることが見て取れる。具体的にどれくらい小さいかを調べるために元の式に代入し直すと、
$$\begin{align*}1 &= \cos\left(\frac{\pi}{2} (2n + 1 + \epsilon_n)\right) \cdot \mathrm{cos h}\left(\frac{\pi}{2} (2n + 1 + \epsilon_n)\right) \\1&\approx -(-1)^{n}\frac{\pi \epsilon_n}{2}\cdot \frac{1}{2} \exp\left(\frac{\pi}{2} (2n + 1)\right)\end{align*}$$
ということで
$$ \epsilon_n \approx -(-1)^{n}\frac{4e^{-\pi / 2}}{\pi } \exp\left(-n\pi \right) $$
と近似できる。右辺に $n=1$ を代入したときの値は $0.01143788\dots$ であり、前述の $3.0112$ をちゃんと説明できる。
周波数比に共通尺度を入れる(弦について)
12音平均律というのは $\ln 2, \ln 3, \ln 5$ をそれぞれ $12 \cdot \frac{\ln 2}{12}, 19 \cdot \frac{\ln 2}{12}, 28 \cdot \frac{\ln 2}{12}$ として近似して得られるのであった。つまり、$\ln 2$ の長さの棒・$\ln 3$ の長さの棒・$\ln 5$ の長さの棒が手元にあるとき、$\ln 2$ を12等分して得られた棒を整数本使うと、わりと精度良く $\ln 3$ や $\ln 5$ を測ることができる、ということである。
さて、この「12等分が比較的いい感じの結果を与える」というのはどのように定量化してやればよいのだろうか。一般に、長さ $1, b_1, b_2$ の棒があったときに、「長さ $1$ の棒を $ n $ 等分して共通尺度として用いることは、 $ m $ 等分して共通尺度として用いることよりも適切である」というのはどうやって定式化すべきだろうか。
直観的には、「$nb_1$ と $nb_2$ はともに整数に近くて、$ mb_1 $ と $ mb_2 $ はそれほど整数に近くない」ということを表現したい。ということで、二乗誤差を足し合わせた $ \sum_{i} (n b_i - \operatorname{round}(n b_i))^2 $ を小さくすることを考えてみる。これを「相対誤差」とでも呼ぶなら、これを $n^2$ で割ったものは「絶対誤差」と呼べるだろう。
1 : 2 : 3 : 4 : 5 の周波数比について、実際にプロットしてみるとこの通り。
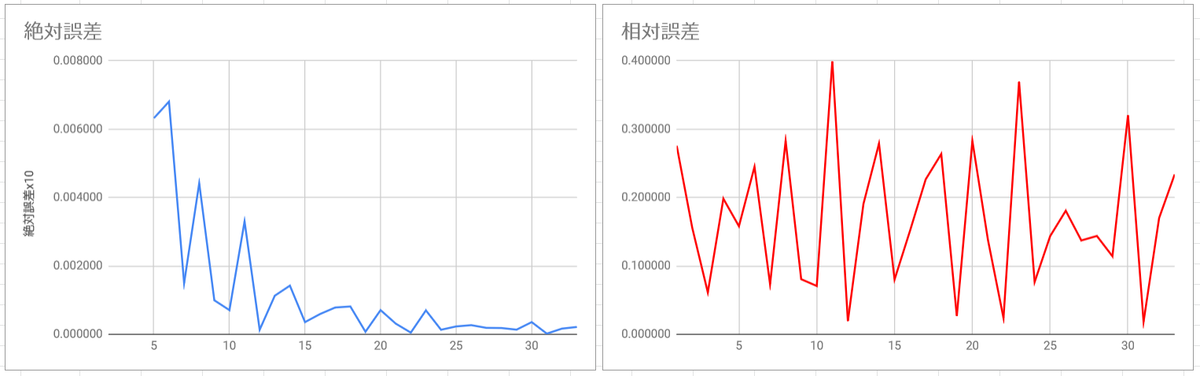
「良い」とされている12分割・19分割・22分割・31分割がこの評価方法で明確な谷として現れることは、この評価方法がわりと有効であることを示唆する。
周波数比に共通尺度を入れる(長い板について)
さて、評価方法が決まったので、さっそく長い板の周波数比についてもやってみよう。
a₁² : a₂² : a₃² : a₄² : a₅² ≒ 3.0112² : 4.9995² : 7² : 9² : 11² の周波数比について、実際にプロットしてみると、
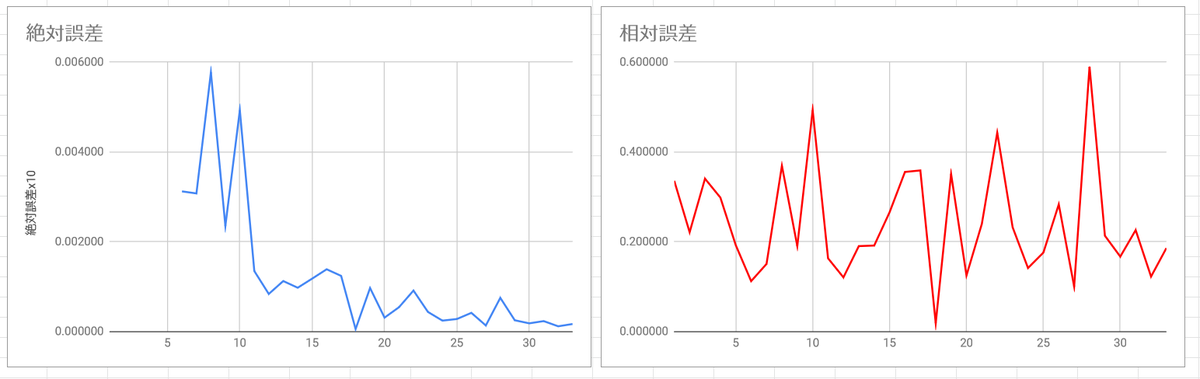
とまあ、18分割だけが突出してものすごく良いということが判明する。この共通尺度 $\left(\frac{a_2^2}{a_1^2}\right)^{1/18} = 1.0579\dots$ はセントに直すと$97.52$セントで、まあ12音平均律の半音よりちょっと狭いかなとなる。1200セントを$97.52$セントで割ると12.3なので、「12.3音平均律」みたいな呼び方をするとウケがいいのかもしれない。