理想的な弦ではなく、理想的な長い板を叩いたときの周波数比に由来する「12.3音平均律」
概要
12音平均律というのは、理想的な弦の振動による周波数比が 1 : 2 : 3 : 4 : 5 : 6 : ... となることと、$2^{7/12} = 1.4983\dots \approx \frac{3}{2}$ および $2^{4/12} = 1.2599\dots \approx \frac{5}{4}$ であることに由来する。完全八度を12分割して得られる代物を共通尺度にすることで、そいつを7つ集めて純正完全五度っぽいものが、そいつを4つ集めて純正長三度っぽいものが再現できてうれしい、というのが12音平均律の根拠である。
さて、では「理想的な弦の振動」ではなくて「理想的な長い板の振動」ならどうであろうか。あ、今回は自由端だけ扱うこととする。
結論を先に言うと、周波数比は 3.0112² : 4.9995² : 7² : 9² : ... になる。この周波数比に言及している文献はわりとあったが、導出してるやつがなかなか見つからずに私が苦労したのでまずはこれの導出をしてから、「12.3音平均律」の提唱に移りたい。
周波数比の導出
微分方程式
オイラー・ベルヌーイの梁理論というやつを使うと、長さ $L$ の梁が材料においても断面の形においても一様である場合、たわみ $w(x, t)$ （$x$ は梁の伸びている方向に沿って定義された座標）の挙動を表す微分方程式は
$$EI\frac{\partial^4 w}{\partial x^4} = \left(- \frac{\partial^2 w}{\partial t^2} \right)\rho A$$
と書ける。ここで $\rho$ [kg/m³] は素材の密度、$A$ [m²] は梁の断面積。$EI$ [N･m²] は曲げ剛性と言われる量であり、材質により決まる弾性率 $E$ [Pa] と、断面の形によって決まる量である面積の第二モーメント $I$ [m⁴] を掛け合わせたものであるらしい。重力加速度は無視したが、欲しい場合はカッコでくくった $- \frac{\partial^2 w}{\partial t^2} $ の項にさらに重力加速度を足せばいい。
境界条件
さて、二階微分というのは曲線が局所的にどれくらい強く曲がっているかを表すわけで、たわみの $x$ についての二階微分 $\frac{\partial^2 w}{\partial x^2}$ は両端 $x=0$ と $x=L$ でゼロになる。
自由端なので、両端での剪断応力もゼロになる。したがってたわみの $x$ についての三階微分も両端でゼロである。
方程式を解く
$$\left(EI\frac{\partial^4 }{\partial x^4} + \rho A \frac{\partial^2 }{\partial t^2}\right) w = 0$$
を解くために、まず $w(x,t) = X(x)T(t)$ という形の解を仮定して
$$\frac{EI}{\rho A} \frac{1}{X}\frac{d^4 X}{d x^4} = - \frac{1}{T}\frac{d^2 T}{d t^2}$$
どうせ $T$ は角振動数 $\omega$ の三角関数で、したがって $\frac{EI}{\rho A} \frac{1}{X}\frac{d^4 X}{d x^4} = \omega^2$ となればよい。 $k = \left(\frac{\rho A \omega^2}{EI}\right)^{1/4}$ と置いて $\frac{d^4 X}{d x^4} = k^4X$ と書いてやれば、
$$X = \alpha \mathrm{cos h}(kx) + \beta \mathrm{sin h}(kx) + \gamma \cos(kx) + \delta \sin(kx)$$
になることがすぐにわかる。さて境界条件。
$X'' = k^2 (\alpha \mathrm{cos h}(kx) + \beta \mathrm{sin h}(kx) - \gamma \cos(kx) - \delta \sin(kx))$ と $X''' = k^3 (\alpha \mathrm{sin h}(kx) + \beta \mathrm{cos h}(kx) + \gamma \sin(kx) - \delta \cos(kx))$ が $x=0$ と $x=L$ の両端でゼロになる必要があるので、
$$\begin{pmatrix}1 & 0 & -1 & 0 \\ \mathrm{cos h} kL & \mathrm{sin h} kL & -\cos kL & -\sin kL \\ 0 & 1 & 0 & -1 \\ \mathrm{sin h} kL & \mathrm{cos h} kL & \sin kL & -\cos kL \end{pmatrix} \begin{pmatrix}\alpha \\ \beta \\ \gamma \\ \delta \end{pmatrix} = \begin{pmatrix}0 \\ 0 \\ 0 \\ 0\end{pmatrix}$$
第一行と第三行（つまり $x=0$ での境界条件）を見ると $\alpha = \gamma$ と $\beta = \delta$ が分かるので、
$$\begin{pmatrix} \mathrm{cos h} kL -\cos kL& \mathrm{sin h} kL -\sin kL \\ \mathrm{sin h} kL + \sin kL & \mathrm{cos h} kL - \cos kL \end{pmatrix}\begin{pmatrix}\alpha \\ \beta \end{pmatrix} = \begin{pmatrix}0 \\ 0 \end{pmatrix}$$
ここで
$$\begin{align*} \det \begin{pmatrix} \mathrm{cos h} kL -\cos kL& \mathrm{sin h} kL -\sin kL \\ \mathrm{sin h} kL + \sin kL & \mathrm{cos h} kL - \cos kL \end{pmatrix} &= ( \mathrm{cos h} kL -\cos kL )^2 - (\mathrm{sin h} kL - \sin kL)(\mathrm{sin h} kL + \sin kL)\\
&= \cos^2 kL - 2\cos kL \mathrm{cos h} kL + \mathrm{cos h}^2 kL - \mathrm{sin h}^2 kL + \sin^2 kL \\
&= 2 - 2\cos kL \mathrm{cos h} kL\end{align*}$$
であることに着目すると、$\cos kL \ \mathrm{cos h} kL - 1 = 0$ でない限り先ほどの方程式に非自明解が存在するはずがない。
これをプロットしてみると、
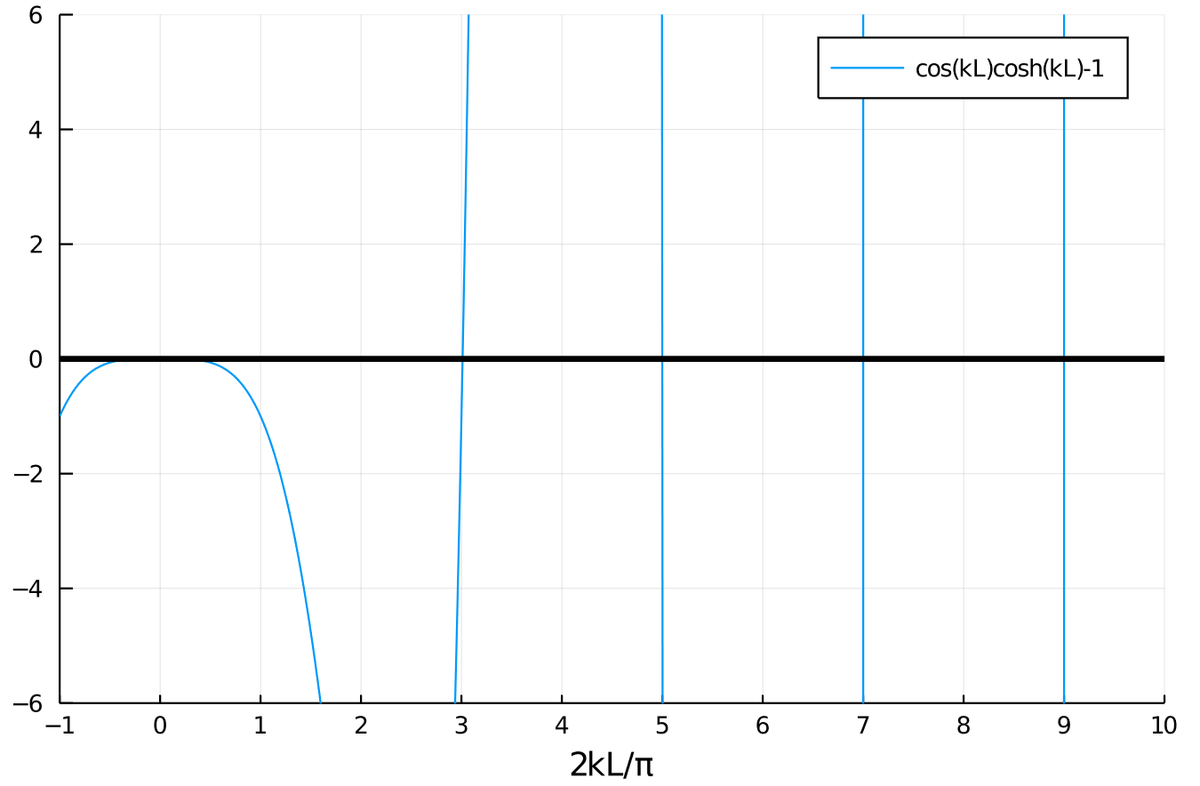
お、3 : 5 : 7 : 9 の謎が見えてきた。
近似
ということで、 $\frac{2kL}{\pi}$ は $3, 5, 7, \dots$ にかなり近いっぽいので、これを評価するために $a_n$ を$1 = \cos(\pi a/2)\ \mathrm{cos h}(\pi a/2)$ の $n$番目の正の解とすると、グラフから $\epsilon_n = a_n - (2n+1)$ が非常に小さい値であることが見て取れる。具体的にどれくらい小さいかを調べるために元の式に代入し直すと、
$$\begin{align*}1 &= \cos\left(\frac{\pi}{2} (2n + 1 + \epsilon_n)\right) \cdot \mathrm{cos h}\left(\frac{\pi}{2} (2n + 1 + \epsilon_n)\right) \\1&\approx -(-1)^{n}\frac{\pi \epsilon_n}{2}\cdot \frac{1}{2} \exp\left(\frac{\pi}{2} (2n + 1)\right)\end{align*}$$
ということで
$$ \epsilon_n \approx -(-1)^{n}\frac{4e^{-\pi / 2}}{\pi } \exp\left(-n\pi \right) $$
と近似できる。右辺に $n=1$ を代入したときの値は $0.01143788\dots$ であり、前述の $3.0112$ をちゃんと説明できる。
周波数比に共通尺度を入れる（弦について）
12音平均律というのは $\ln 2, \ln 3, \ln 5$ をそれぞれ $12 \cdot \frac{\ln 2}{12}, 19 \cdot \frac{\ln 2}{12}, 28 \cdot \frac{\ln 2}{12}$ として近似して得られるのであった。つまり、$\ln 2$ の長さの棒・$\ln 3$ の長さの棒・$\ln 5$ の長さの棒が手元にあるとき、$\ln 2$ を12等分して得られた棒を整数本使うと、わりと精度良く $\ln 3$ や $\ln 5$ を測ることができる、ということである。
さて、この「12等分が比較的いい感じの結果を与える」というのはどのように定量化してやればよいのだろうか。一般に、長さ $1, b_1, b_2$ の棒があったときに、「長さ $1$ の棒を $ n $ 等分して共通尺度として用いることは、 $ m $ 等分して共通尺度として用いることよりも適切である」というのはどうやって定式化すべきだろうか。
直観的には、「$nb_1$ と $nb_2$ はともに整数に近くて、$ mb_1 $ と $ mb_2 $ はそれほど整数に近くない」ということを表現したい。ということで、二乗誤差を足し合わせた $ \sum_{i} (n b_i - \operatorname{round}(n b_i))^2 $ を小さくすることを考えてみる。これを「相対誤差」とでも呼ぶなら、これを $n^2$ で割ったものは「絶対誤差」と呼べるだろう。
1 : 2 : 3 : 4 : 5 の周波数比について、実際にプロットしてみるとこの通り。
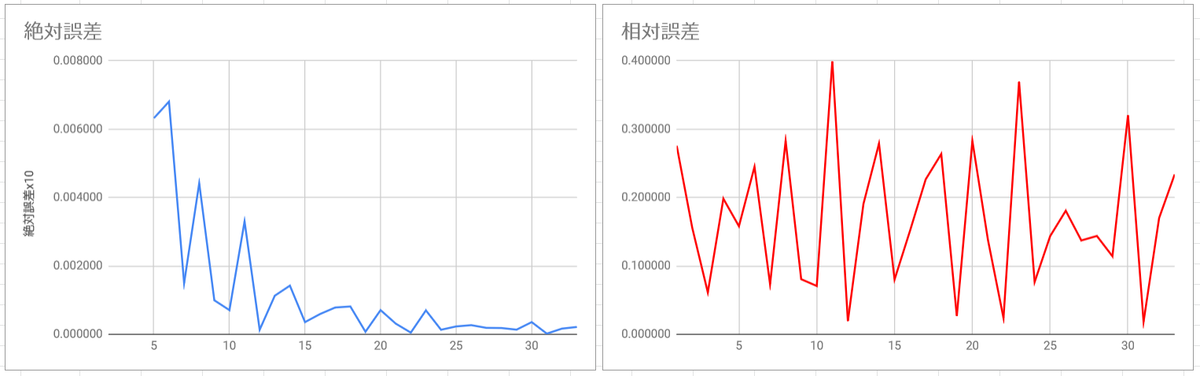
「良い」とされている12分割・19分割・22分割・31分割がこの評価方法で明確な谷として現れることは、この評価方法がわりと有効であることを示唆する。
周波数比に共通尺度を入れる（長い板について）
さて、評価方法が決まったので、さっそく長い板の周波数比についてもやってみよう。
a₁² : a₂² : a₃² : a₄² : a₅² ≒ 3.0112² : 4.9995² : 7² : 9² : 11² の周波数比について、実際にプロットしてみると、
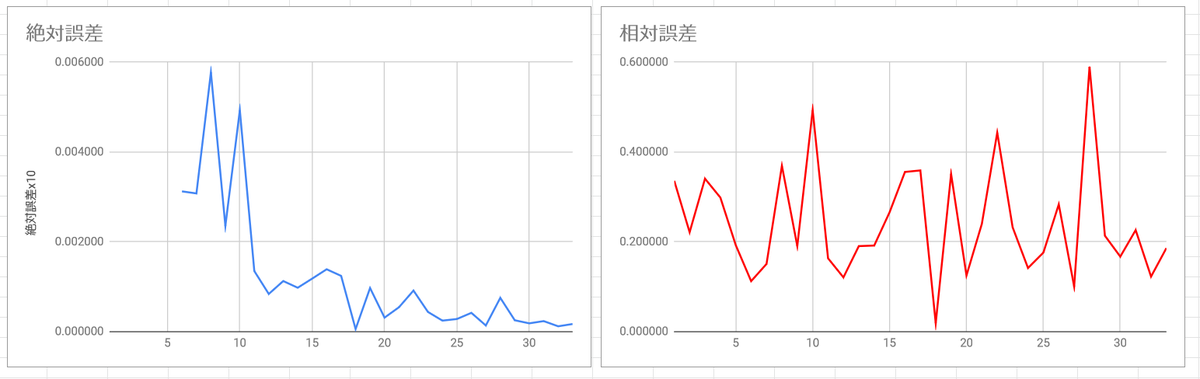
とまあ、18分割だけが突出してものすごく良いということが判明する。この共通尺度 $\left(\frac{a_2^2}{a_1^2}\right)^{1/18} = 1.0579\dots$ はセントに直すと$97.52$セントで、まあ12音平均律の半音よりちょっと狭いかなとなる。1200セントを$97.52$セントで割ると12.3なので、「12.3音平均律」みたいな呼び方をするとウケがいいのかもしれない。
語学と私 (part2)
おことわり
↑ の続編です。読んでない人は先に読んでおくことをおすすめします。
本文
ということで久々に語学というものを真面目にやりました。私という人間は根が不真面目でございますので、「語学を真面目にやる」というのは「真面目にやらないと不利益がそこそこ発生する環境に、置かなくてもいいのに自らを置く」とだいたい同義です。結果としてどうなったかはまあ察せている方もいるかと思いますが、「真面目にやらないと不利益がちょっと発生する環境に、置かなくてもいいのに自らを置いたが、やっぱり真面目にはやらなかったので不利益がちょっと発生した」というオチになるわけです。
じゃあナワトル語の授業を履修したことを後悔しているかというと、もう全くもってそんなことはありません。もともと私は後悔というものをする頻度が極端に低い人間ではありますがそれとは関係なく、むしろ「ナワトル語の授業を日本にいながら受ける」という非常に珍しい体験をすることができたというだけでもスタンフォード大学に所属した甲斐があったとまで感じています。
ナワトル語について
そもそも「ナワトル語」と聞いてピンとくる方ばかりではない（というか、どう考えてもピンと来ない方ばかりである）（と思ったがわざわざこんなタイトルのブログを読む人なら知ってるのが普通かもしれない）（とも思うがまあ一応書いておこう）と思うので概略だけでも。
ナワトル語の授業を受けている旨を口頭（こんなご時世なのでほとんどが Discord か VRChat、たまに Zoom）で言及する際に、テンプレ会話パターンとして使っていたのは以下の通り。
単語帳を回す私「ニｸネキ・シキーｼマティ・セー・ノテキｼポﾎ。」*1
人「なにやってるんですか」
私「ナワトル語の単語帳回してます」
人「ナワトル語ってなんですか」
私「アステカ帝国の公用語*2で、今でも160万人ぐらいが話してるみたいですね」
人「はえー」
まあ雑談であまり長々と語ってもしょうがないわけで、これぐらいの簡潔さでまとめて話すことになるわけですね。アステカ帝国って単語はなんだかんだ皆さんご存知なのできれいにまとまる。
さて、ブログというのは対話とは違って私が一方的に長々と語る場なので、もうちょい書くことにしましょう。
まず、皆さん「アステカ」と「マヤ」の違いって分かります？そんなあなたにおすすめなのが ↓ の動画。（私はこの動画見るまで全然区別ついてませんでした。）「英語動画見るのつらい」って人は冒頭の20秒だけでも見といてください。
ナワトル語はこの「アステカ」の方です。
ナワトル語と私
ナワトル語について最初に目にしたのは、多分「ナワトル語には tl として綴られる音があって、こいつがおもしろい」みたいな話が日本語版 Wikipedia に書いてあったのを見たときな気がします（聞いてみたい方は、 tlahtlaniliztli. | Nahuatl Dictionary とかの音声を聞いてみるといいと思います）。
なお、実際にこれを発音してみたい方は、
- まず『タ』を言おうとし、寸止めする
- すると舌が口の上部（上の前歯の周辺）にくっつく。
- さて、普通『タ』を言うときは、このあと「下顎が下がることによって口が開き、舌もそれについていって口の下部に行く」という動きをするはずである（それを意識したことはないかもしれないが）。
- しかしながら、今回は舌の先端を意地でも上前歯から外さずに息を吐こうとしてみる。そうやって一瞬息が吐けたら、そのあとは意地を張るのをやめ、普通に『タ』を言うときの挙動をしてみる
をやると、だいぶいい感じの tla が言えると思います。*3
その次に目にしたのは多分国際言語学オリンピック2015（ブルガリア大会）に出場したときのことで、 ナワトル語の数詞体系に関する問題とかをブルガリアに行って解きました。（問題文はここにあります。）（あ、上記問題をネタバレ無しで解いてみたいという方は、このブログを読み進める前に解いておいてください。後でネタバレ書きますので。）
それから数年が過ぎ、私はTwitterを始め、2017年12月にはこんなツイートをRTしていたようです。
古典ナワトル語、まず挨拶するために敬語活用に必要な充当形と使役形を覚えて、そのために動詞の価数と再帰形と初級の難関である3群動詞の語幹交替をマスターしないと、人に会って挨拶もできないあたりが、語学としての不人気の理由なのかもな #これでもナワトル語はメソアメリカで一番簡単な言語です
— Mitchara (@Mitchara) 2017年12月5日
さらに数年が経ったある日（具体的には2019年8月18日）のこと。
国際先住民語年、そういえば今年はコルテスのメキシコ上陸500周年だからだろうか。それについてはまあ昨日今日先住民語を始めたわけではないので何も言うことはありません。ありませんが、ナワトル語はわずか5000円で習得できるということは申し上げておきます https://t.co/jS9lRbn0Aa
— Mitchara (@Mitchara) 2019年8月18日
というツイートが流れてきて、さっそく Launey, M., & Mackay, C. S. (2011). An introduction to classical Nahuatl. New York: Cambridge University Press. の Kindle版を買いました。
かなしいことに、Kindle版は組版がつらいことになっており、読むに耐えませんでした。
これKindleで買ったらマクロンが画像で入っててめちゃめちゃ読みにくかったので、みなさん紙で買いましょう https://t.co/LhY9S9lg2G
— jekto.vatimeliju@hsjoihs@.sozysozbot. (@sosoBOTpi) 2019年10月5日
ということで、 2019年10月には紙版も購入。
それと並行して、創作自然言語などを行う集まりがスタンフォード大学に存在することを知り、参加。 *4
なんかこういうものがあるらしいので顔を出してみようかと pic.twitter.com/GrnuZkqdyt
— jekto.vatimeliju@hsjoihs@.sozysozbot. (@sosoBOTpi) 2019年10月24日
すると、まあやはり言語の話で盛り上がるわけでして。
早速ラテン語とナワトル語とクウェンヤの話が始まった
— jekto.vatimeliju@hsjoihs@.sozysozbot. (@sosoBOTpi) 2019年10月24日
この回だったかそれ以降の回だったかは覚えていませんが、手元にあった言語周りの本を全部（当然ナワトル語の文法書を含む）カバンに詰めて持参したりして場を盛り上げたりもしたはずです（「あれ、受身ってどう表現するの？」みたいな質問にその場で開いて答えることができてたのしかったです）。
さて、その後の何らかのタイミングで文法書の全ページを眺める作業（この行為に「読む」という動詞を用いていないことに注意。つまり眺めただけで読了後になんも覚えていない様を表す。）を行ったことは記憶にあるのですが、いつだったのかを一切覚えていません。2020年3月からロックダウンして、2020年6月に日本にこっそり帰ってきたのは確実だけれど、読了は日本に帰ってきてからだったかなぁ～？んー、自信がないです。
それはともかく、文法書の全ページを眺める作業を行った以上、せっかくナワトル語が開講されているならそれを履修するしかないわなということで、
前回 ↑ 書いたように、ナワトル語の授業を取ることにしてみました。
前置きが長くなりすぎた
えーと、この記事はもともと「IDIEZという（比較的思想の強い）団体が提供するナワトル語教育を2学期間受けた感想」というタイトルにしようと思っていたんですが、IDIEZという語すら登場せず4000文字に達しようとしているので、一旦記事を分けます。
*1:「私の友達に会って欲しい」。興味のある方のために書いておくと、Nicnequi xiquīxmati cē notequixpoh. は nicnequi /nikneki/ (ニｸネキ) 【ni-「私が」 + k-「彼・彼女・それを」+ neki「欲する」】、xiquīxmati /šikiːšmati/ (シキーｼマティ) 【ši-「あなたが～しろ」 + k-「彼・彼女・それを」+ īšmati「～と会う」】、cē /seː/ (セー)「ひとつの」、notequixpoh /notekišpoh/ (ノテキｼポﾎ) 【no-「私の」 + tekišpoh「友達」 】から構成される。
*2: lingua franca という表現は一般人に通じるわけないので
*3:「あれ？ [t͡ɬ] ってそんな音なの？」と疑問に思った方のために、ツイートを一つ貼っておきます。
IPAというかその運用についていうと、なんでみんなナワトル語の tl 音を [tɬ] って書くの。IPAには [tˡ] の記号があるし、それ使えばナバホ語の tł / dl / tł' だってちゃんと書き分けられるんだから、普通にそれ使えばよくない？ ねえ？
— Mitchara (@Mitchara) 2018年10月21日
*4:普通「人工言語」と呼ばれるタイプの創作活動。↓ に従い、ここでは「創作自然言語」表記を用いる。
ぼくが「創作自然言語」っていう単語を使うのは、ぼくは情報系の人間なので、「人工言語」っていうと先に「工学言語/プログラミング言語/etc.」を思い浮かべる方がTLに多いからなのですよね
— ゆーちき (@yuchiki1000yen) 2020年5月30日
ちょっと長ったらしいけど、まあ紛らわしさは減るかなと思って
ピタゴラスで √n な螺旋
概要
皆さんは、以下のような図形を見たことがあるだろうか。私はある。
如何なる機会にこれを見たのかはもはや定かではないが、たしか作図可能数の議論をする際に「自然数の平方根についてはこのように作図することができる」という例示としてなんらかの本で出てきていた気がする。直角を作図できるので直角三角形が作図でき、一辺の長さが1となるような直角三角形を積み重ねれば√nが作図できるということである。
この図のことは長らく忘れていたが、スーパーマリオ64 RTA/TAS用のWikiを今日なにげなく読んでいたところ、
この図のことを思い出した。ということで、ちょっとこいつについて考えてみる。
挙動
まず $f\left(k\right)=\sum_{n=1}^{k}\mathrm{a r ctan}\left(\frac{1}{\sqrt{n}}\right)$ を定義してやることにより、各頂点は極座標上で $(r, \theta) = (\sqrt{N}, f\left(N-1\right))$ と書ける（$N=0$とすると原点もカバーされていてくれたりする）。ということで $f(k)$ を調べてやることで挙動がわかる。
とりあえず雑に見積もる。$\sum_{n=1}^{k}\mathrm{a r ctan}\left(\frac{1}{\sqrt{n}}\right)$ というのはだいたい$\sum_{n=1}^{k}\frac{1}{\sqrt{n}}$ である。こいつはだいたい $\int_{1}^{k}\frac{1}{\sqrt{x}}dx$ であり、つまり $2\sqrt{k}$ ぐらいの速度で成長しそうだ。つまり $N$ が大きいときには $(r, \theta) \approx (\sqrt{N}, 2\sqrt{N})$ みたいな感じであり、$r = \frac{\theta}{2}$ なアルキメデス螺旋に似た振る舞いをしてくれそうである。
詳しい挙動
$f(k)$ はだいたい $2\sqrt{k}$ であることがわかった。さて $\lim_{k \to \infty} \left(f(k) - 2\sqrt{k} \right)$ って存在するんだろうか。desmosで実験してみた限りでは、しそう。ということで計算したい。
えー arctan をテイラー展開してやる。ただし $f(k)$ の初項は展開したやつが絶対収束ではないので、それだけ除外してやると、
$$f\left(N\right)=\sum_{n=1}^{N}\mathrm{a r ctan}\left(\frac{1}{\sqrt{n}}\right) = \frac{\pi}{4} + \sum_{n=2}^{N}\mathrm{a r ctan}\left(\frac{1}{\sqrt{n}}\right) = \frac{\pi}{4} + \sum_{n=2}^{N}\sum_{l=0}^\infty \frac{(-1)^l \left(\frac{1}{\sqrt{n}}\right)^{1 + 2 l}}{1 + 2 l}$$
総和を入れ替えたやつは
$$ \frac{\pi}{4} +\sum_{l=0}^\infty \frac{(-1)^l}{1 + 2 l} \sum_{n=2}^{N}n^{-l - 1/2}$$
ここで $l > 0$ の場合は $\sum_{n=2}^{N}n^{-l - 1/2}$ というのは $N \to \infty$ で $\zeta\left(l + \frac{1}{2}\right) - 1$ に収束する。$l = 0$ のときのはなんか Lampret, V. An accurate approximation of zeta-generalized-Euler-constant functions. centr.eur.j.math. 8, 488–499 (2010). https://doi.org/10.2478/s11533-010-0030-7 で the zeta-generalized-Euler-constant function という名前で呼ばれ、https://en.wikipedia.org/w/index.php?title=Euler%E2%80%93Mascheroni_constant&oldid=997546999 で Euler's generalized constantsと呼ばれている以下のやつ：
$$\gamma(s) = \lim_{n\to\infty}\left[\sum_{k=1}^{n} \left(\frac{1}{k^s} - \int_{k}^{k+1} \frac{dx}{x^s}\right)\right]$$
が使えそうである。結局 $\frac{\pi}{4}$ をバラさないと綺麗にならないので、絶対収束性を忘れて $\frac{\pi}{4}$ を解体することで、
$$f\left(N\right) - \int_{1}^{N+1} \frac{1}{\sqrt{x}}dx \to \gamma\left(\frac{1}{2}\right) + \sum_{l=1}^\infty \frac{(-1)^l}{1 + 2 l} \zeta\left(l + \frac{1}{2}\right) $$
$$f\left(N\right) - (2\sqrt{N+1}-2) \to \gamma\left(\frac{1}{2}\right) + \sum_{l=1}^\infty \frac{(-1)^l}{1 + 2 l} \zeta\left(l + \frac{1}{2}\right) $$
$$f\left(N\right) - 2\sqrt{N} \to -2 + \gamma\left(\frac{1}{2}\right) + \sum_{l=1}^\infty \frac{(-1)^l}{1 + 2 l} \zeta\left(l + \frac{1}{2}\right) $$
な気になれる。
うーん、なんも綺麗にならん！ｗ
2次元調和振動子（古典力学）
概要
ベルトランの定理により、軌道が必ず閉軌道になるような中心力ポテンシャルというのは調和振動子とケプラー問題だけであることが知られている。ケプラー問題においては、エネルギーと角運動量だけでなく、離心率ベクトル（ルンゲ＝レンツベクトルの定数倍）という幾何学的な意義のあるベクトルが保存量となるということが知られている。じゃあ2次元調和振動子のときには何が保存されるのか。気になったがググってもいい感じの資料がヒットしない（みんな量子の方の話ばかりしとる）ので、自分で考えてみることにした。
2次元調和振動子
初期位置 $\vec{X} = (X, Y)$, 初速度 $\vec{V} = (V_x, V_y)$ で質量 $m (>0) $ の粒子を調和振動子ポテンシャル $U(x,y) = \frac{1}{2}m\omega^2 (x^2+y^2)$（ただし $\omega \not= 0$） の中に投げ込んだとき、粒子は時刻 $t$ には位置 $\left(X\cos\omega t + \frac{V_{x}}{\omega}\sin\omega t,Y\cos\omega t+ \frac{V_{y}}{\omega}\sin\omega t\right)$ にある。時間に対する並進対称性があり、回転対称性もある系なので、総エネルギー $ \frac{1}{2}m(v_x^2+v_y^2) + \frac{1}{2}m\omega^2 (x^2+y^2)$ と角運動量 $mx v_y - my v_x$ は保存量となる。角運動量が非ゼロなら軌道は中心を原点とした円か楕円であり、いずれにしても閉軌道をなす。
以下長いので、まずはdesmosで書いた初期位置と初速度いじれるやつで遊んでみていただきたい。
ここで、楕円の2つの直交する軸を表す青い2直線は、$\left(x^{2}-y^{2}\right)\ \left(\frac{V_{x}}{\omega}\frac{V_{y}}{\omega}+XY\right)+\ xy\left(\frac{V_{y}^{2}-V_{x}^{2}}{\omega^{2}}+\left(Y^{2}-X^{2}\right)\right)=0$ として描画している。初期条件だけに基づいて、楕円の幾何学的特徴を表す存在を描画できているようだ。ということで、こいつについて調べてみよう。
証明パート
補題0
実数$A, B$ に対して、写像 $(x,y) \mapsto A\left(x^{2}-y^{2}\right)+2Bxy$ を考える。$A=B=0$ であればあらゆる $(x,y)$ に対しこの写像は $0$ を返す。それ以外の場合、2つの直交する軸が存在して、それら2軸上のベクトルに対してのみこの写像は $0$ を返す。
補題0の証明のsketch
$A=B=0$ については自明。そうでなければ、$A\left(x^{2}-y^{2}\right)+2Bxy=0$ を $\begin{pmatrix} x & y\end{pmatrix} \begin{pmatrix} A & B \\ B & -A \end{pmatrix} \begin{pmatrix} x \\ y\end{pmatrix} = 0 $ と書くと、$\begin{pmatrix} A & B \\ B & -A \end{pmatrix}$ の行列式は $-A^2-B^2 < 0$.
$\begin{pmatrix} A & B \\ B & -A \end{pmatrix}$ は実対称行列なので直交行列により対角化可能で、元のトレースが $0$ なのだから対角行列もトレースが $0$、元の行列式が非ゼロなのだから対角行列も行列式が非ゼロ。つまり直交行列 $P$ と実数 $C \not= 0$ が存在して、$A\left(x^{2}-y^{2}\right)+2Bxy=0$ を $\begin{pmatrix} x & y\end{pmatrix}P^T \begin{pmatrix} C & 0 \\ 0 & -C \end{pmatrix} P \begin{pmatrix} x \\ y\end{pmatrix} = 0 $ と書ける。直交する2ベクトル $P^{-1} \begin{pmatrix} 1 \\ 1\end{pmatrix} $ と $P^{-1} \begin{pmatrix} 1 \\ -1\end{pmatrix} $、およびこいつらのスカラー倍だけがこの式を成り立たせることは簡単に確認できる。
補題1
初期条件が円軌道（粒子が原点に居座る場合も半径$0$の円軌道と見なす）を与えることと、写像 $ (x,y) \mapsto \left(x^{2}-y^{2}\right)\left(\frac{V_{x}}{\omega}\frac{V_{y}}{\omega}+XY\right)+ xy\left(\frac{V_{y}^{2}-V_{x}^{2}}{\omega^{2}}+\left(Y^{2}-X^{2}\right)\right)$ が恒等的に$0$を与える写像となることとは同値である。
補題1の証明のsketch
初期条件が円軌道を与えるならば、中心が原点の円軌道であるので、角運動量保存により角速度は一定である。よって等速円運動である。周期の一意性より角速度$\omega$の等速円運動であるので、初期位置 $\vec{X} = (X, Y)$ と 初速度 $\vec{V} = (V_x, V_y)$ は直交し、 $|\vec{V}| = \omega|\vec{X}|$ である。 つまり $V_x + iV_y= \pm i \omega (X + iY)$ であるので、両辺を2乗すると $(V_x^2 - V_y^2) + 2iV_xV_y= - \omega^2 (X^2 - Y^2 + 2iXY)$ であり、実部どうしと虚部どうしを比較すると $V_x^2 - V_y^2 = - \omega^2 (X^2 - Y^2)$ と $2V_xV_y= - 2XY\omega^2$ が分かる。したがって $\frac{V_{x}}{\omega}\frac{V_{y}}{\omega}+XY = 0$ と $\frac{V_{y}^{2}-V_{x}^{2}}{\omega^{2}}+\left(Y^{2}-X^{2}\right) = 0$ が分かるので、写像 $ (x,y) \mapsto \left(x^{2}-y^{2}\right)\left(\frac{V_{x}}{\omega}\frac{V_{y}}{\omega}+XY\right)+ xy\left(\frac{V_{y}^{2}-V_{x}^{2}}{\omega^{2}}+\left(Y^{2}-X^{2}\right)\right)$ は恒等的に$0$を与える写像となる。
逆に、写像 $ (x,y) \mapsto \left(x^{2}-y^{2}\right)\left(\frac{V_{x}}{\omega}\frac{V_{y}}{\omega}+XY\right)+ xy\left(\frac{V_{y}^{2}-V_{x}^{2}}{\omega^{2}}+\left(Y^{2}-X^{2}\right)\right)$ が恒等的に$0$を与える写像であれば、補題0より $\frac{V_{x}}{\omega}\frac{V_{y}}{\omega}+XY = 0$ と $\frac{V_{y}^{2}-V_{x}^{2}}{\omega^{2}}+\left(Y^{2}-X^{2}\right) = 0$ が分かる。ここから$(V_x^2 - V_y^2) + 2iV_xV_y= - \omega^2 (X^2 - Y^2 + 2iXY)$ であり、$V_x + iV_y= \pm i \omega (X + iY)$ であり、原点中心の等速円運動である。
補題2
角運動量が $0$であり、粒子が原点に居座るのでないならば、写像 $ (x,y) \mapsto \left(x^{2}-y^{2}\right)\left(\frac{V_{x}}{\omega}\frac{V_{y}}{\omega}+XY\right)+ xy\left(\frac{V_{y}^{2}-V_{x}^{2}}{\omega^{2}}+\left(Y^{2}-X^{2}\right)\right)$ は、振動方向に平行または垂直なベクトルが入力されたときのみ $0$ を出力する写像となる。
補題2の証明のsketch
角運動量が $0$ であるなら $\vec{X}$ と $\vec{V}$ は平行（含ゼロベクトル）である。粒子は原点に居座っていないので、非0な複素数 $Z$ と少なくとも片方は非0な実数 $a$, $b$ が存在して $X + iY = aZ$, $\frac{V_x}{\omega} + i\frac{V_y}{\omega} = bZ$ と書ける。そうすると $\frac{V_{x}}{\omega}\frac{V_{y}}{\omega}+XY = \frac{1}{2}\mathrm{Im}(b^2Z^2) + \frac{1}{2}\mathrm{Im}(a^2Z^2) = \frac{a^2+b^2}{2} \mathrm{Im}(Z^2)$ と $\frac{V_{y}^{2}-V_{x}^{2}}{\omega^{2}}+\left(Y^{2}-X^{2}\right) = -\mathrm{Re}(b^2Z^2)-\mathrm{Re}(a^2Z^2) = -(a^2+b^2)\mathrm{Re}(Z^2)$ が成り立つので、$z = x + iy$ と置けば $\left(x^{2}-y^{2}\right)\left(\frac{V_{x}}{\omega}\frac{V_{y}}{\omega}+XY\right)+ xy\left(\frac{V_{y}^{2}-V_{x}^{2}}{\omega^{2}}+\left(Y^{2}-X^{2}\right)\right) =\mathrm{Re}(z^2)\frac{a^2+b^2}{2} \mathrm{Im}(Z^2)-(a^2+b^2)\mathrm{Re}(Z^2)\frac{1}{2}\mathrm{Im}(z^2)$ であり、こいつは $-\frac{a^2+b^2}{2}|Z^4|\mathrm{Im}\left(\frac{z^2}{Z^2}\right)$ と書ける（一般に $bc-ad = |c+di|^2 \frac{bc-ad}{c^2+d^2} = |c+di|^2 \mathrm{Im}(\frac{a+bi}{c+di})$ であることから従う）。 $-\frac{a^2+b^2}{2}|Z^4| \not= 0$ より、例の写像は $\frac{z^2}{Z^2}$ が実数であるときのみ $0$ を出力する写像であり、つまり $\frac{z}{Z}$ が実数または純虚数であるときのみ $0$ を出力する写像であり、$(x,y)$ が $\vec{X}$ と $\vec{V}$ の両方と平行、または両方と垂直、である場合のみに $0$ を出力する写像である。
主定理
楕円軌道であるならば、写像 $(x,y) \mapsto \left(x^{2}-y^{2}\right)\left(\frac{V_{x}}{\omega}\frac{V_{y}}{\omega}+XY\right)+ xy\left(\frac{V_{y}^{2}-V_{x}^{2}}{\omega^{2}}+\left(Y^{2}-X^{2}\right)\right)$ は、楕円の短軸か長軸と平行なベクトルが入力されたときのみ $0$ を出力する写像となる。
主定理の証明のsketch
楕円軌道にならない場合については補題1と補題2で考察した。ということで、角運動量は $0$ ではないし、$\frac{V_{x}}{\omega}\frac{V_{y}}{\omega}+XY$ と $\frac{V_{y}^{2}-V_{x}^{2}}{\omega^{2}}+\left(Y^{2}-X^{2}\right)$ のどちらかは非ゼロである。
$\frac{V_{y}^{2}-V_{x}^{2}}{\omega^{2}}+ Y^{2}-X^{2} = 0$のとき
$\frac{V_{x}}{\omega}\frac{V_{y}}{\omega}+XY$は非ゼロである。写像は $(x,y) \mapsto + xy\left(\frac{V_{y}^{2}-V_{x}^{2}}{\omega^{2}}+\left(Y^{2}-X^{2}\right)\right)$ なので、この写像は $x$ 軸上の点と $y$ 軸上の点に対して、かつそのときのみ、 $0$ を出力する。
$\frac{V_{y}^{2}-V_{x}^{2}}{\omega^{2}}+ Y^{2}-X^{2} \not= 0$のとき
読者への演習課題とする。（まだ書き切れていないので後日書き上げて公開するかもしれません）
語学と私
以下、201920年9月19日に私が書いたメモに加筆したもの。
私はいま新幹線に乗っている。
恥ずかしいことに、
さて日本に帰ってきた。
非帰国生枠で入ったことは幸運であった。まず、日本のいわゆる「
入った学校もこれまた幸運であった。
高3は受験シーズンである。
代わりに育ったのは、当然ながら英語である。
辞書と言ったが、
中古漢語の音韻的体系について良き師をTwitter上で見つけ
大学。第一外国語に英語以外を選べるということを知り、第一外国語をフランス語、第二外国語を韓国朝鮮語として入学手続きを行う。ゆえに、フランス語の映画を見て、電子辞書を怒濤の速度で叩きながら話されるフランス語をなんとか解釈しようとし、発言を求められた際は英作をして頭からフランス語に訳す。確実に今までで一番フランス語をよく使った三ヶ月だったと思う。
ところで、フランス語は場合によっては音声から辞書を引くのがだいぶ難しい。音声ベースで引ける辞書とかないのか。
/sæ̃/ で始まる単語を引きたいときに開く箇所：
— jekto.vatimeliju@hsjoihs@.sozysozbot. (@sosoBOTpi) 2019年9月7日
cein-
cin-
sain-
scin-
sein-
sim- ~ sin-
sym- ~ syn-
大学その2。日本語ができることが卒業要件「語学」を満たすので語学を取らなくていい。ということで、語学をほぼやらずに言語学だけやる生活を3年続けた。「現代ヘブライ語についての文法書を図書館から借り、全ページに目を通し、単語を1個も覚えずに返却する」みたいな。ときたまフランス語会話イベントなどが発生し、私のひどいフランス語を晒すはめになった。
polyglotと言語学者が別概念であることを伝える言い訳と
ファミコン疑似三角波のフーリエ級数展開
概要
http://sketch.txt-nifty.com/blog/2008/12/post-cb2c.htmlによれば、ファミコン音源の「三角波」は実は16段階の階段状で、F E D C B A 9 8 7 6 5 4 3 2 1 0 0 1 2 3 4 5 6 7 8 9 A B C D E F の繰り返しを出力するそうだ。なるほどね。
ということでフーリエ級数展開してみよう。周期$t_0$の三角波の一周期分は$\left\{0<x<\frac{t_{0}}{2}:-1+\frac{4x}{t_{0}},\frac{t_{0}}{2}<x<t_{0}:3-\frac{4x}{t_{0}}\right\}$と書けて（これはdesmos記法の条件分岐。標準的な記法で書くなら$\begin{cases} -1+\frac{4x}{t_{0}} & (0<x<\frac{t_{0}}{2}) \\ 3-\frac{4x}{t_{0}} & (\frac{t_{0}}{2}<x<t_{0}) \end{cases}$ のこと。）、これを16段階に切ってやるには8倍して床関数を噛ませればよくて、それを線形変換して-1~1の範囲におさめると$f(x) = \frac{\operatorname{floor}\left(\left\{0<x<\frac{t_{0}}{2}:-1+\frac{4x}{t_{0}},\frac{t_{0}}{2}<x<t_{0}:3-\frac{4x}{t_{0}}\right\}\cdot8\right)\cdot2+1}{15}$ と書ける。この$f(x)$ をフーリエ級数展開してやればいい。
正の整数$n$について$h(n) = \frac{2}{t_{0}}\int_{0}^{t_{0}}f\left(x\right)\cos\left(\frac{2\pi n x}{t_{0}}\right)dx$ とする。区分定数関数なので簡単に計算できて$$h(n) = \frac{4}{2\pi n}\sum_{l=0}^{15}\left(-1+\frac{2l}{15}\right)\left(\sin\left(\frac{2\pi n\left(l+1\right)}{32}\right)-\sin\left(\frac{2\pi nl}{32}\right)\right)$$シグマを展開すると隣り合う項同士が部分的に打ち消し合うので$$h(n) = \frac{4}{2\pi n}\left(\sin\left(\pi n\right)-\frac{2}{15}\sum_{m=0}^{15}\sin\left(\frac{2\pi m n}{32}\right)\right) $$
整数$n$に対して$\sin\left(\pi n\right) = 0$ である。偶数$n$に対しては$\sum_{m=0}^{15}\sin\left(\frac{2\pi m n}{32}\right)$というのは（$n$が$32$の倍数でないのなら単位円上に等間隔に置かれた点のy座標の総和、$n$が$32$の倍数なら全部ゼロなので）ゼロ。ということでフーリエ級数展開は（収束性とかの議論をすっ飛ばして=を書いてしまうと） $$f(x) = \sum_{k=1}^{\infty}h\left(k\right)\cos\left(\frac{2\pi kx}{t_{0}}\right) = \sum_{k=0}^{\infty}h\left(2k+1\right)\cos\left(\frac{2\pi\left(2k+1\right)x}{t_{0}}\right) $$ sinの和をうまく積和で処理してやることで $$f(x) = \sum_{k=0}^{\infty}-\frac{4}{\pi\left(2k+1\right)}\left(\frac{\sin\left(\frac{\pi\left(2k+1\right)}{2}\right)\sin\left(\frac{15\pi\left(2k+1\right)}{32}\right)}{15\sin\left(\frac{\pi\left(2k+1\right)}{32}\right)}\right)\cos\left(\frac{2\pi\left(2k+1\right)x}{t_{0}}\right)$$ を得る。
メモ用紙はこちら。
実際どんな感じになるのかを見てみよう。2乗して対数取って10倍すればデシベルが出る。
ということで、第3倍音や第5倍音などについてはほぼ差は無いが、疑似三角波の方は例えば第31倍音が-29.83dBあり、これは第5倍音（-28.67dB）に匹敵するというわけか。なるほど。
追記
このサイトにも "a triangle wave generator with a 32-step waveform (16 steps up, 16 steps down)" と書いてあるので、16段階なんでしょう（てきとう）
ATOKを買ったのでAZIKにする on Windows (2020年)
概要
私がかつて使用していて、2020年4月末頃からまた使い出した日本語入力方法として、AZIKというのがある。AZIKというのは、一般的なローマ字テーブル1を微改造したローマ字テーブルである。ローマ字テーブルとは、要するにkyuと入力されたらそれを「きゅ」と解釈せよ、というのを収録している一覧表のことである。
AZIKの特徴として、「-aん」「-iん」「-uん」「-eん」「-oん」と「-aい」「-uう」「-eい」「-oう」が2ストロークで打てるというのがある。具体的には、例えば「-aん」には（QWERTY配列でAの下の）「Z」が、「-oう」には（Oの右の）「P」が当たっているので、
環状構造 → KZJPKPZP
高等教育 → KPTPKYPIKU
などと打つことができる。具体的な仕様については AZIK総合解説書 とか AZIKとは (エイズィックとは) [単語記事] - ニコニコ大百科 とかをどうぞ。個人的には「ぬ」とかが「NF」で打てるのが地味に便利だと思っている。
さて、Google日本語入力でAZIKを使っていたが、諸般の事情でATOKに乗り換えてみることにしてみた。その際、現在のATOKに入れる方法を調べるのに意外と時間がかかったのでメモしておく。
やり方
- ATOK2013,2014用AZIK（拡張ローマ字入力）定義ファイル - とぴやまのブログ（アーカイブ） にある azik/ATOK2014 at master · topiyama/azik · GitHub からSTYファイルをダウンロードしたのち、Ctrl+F12で出る「ATOKプロパティ」から「キー・ローマ字・色」を選択。「スタイル操作(F) ▼」から「スタイルコンバート」を選び、「スタイル」横の「参照」から先ほどダウンロードしたSTYファイルを選択し、「実行」。
終わりに
ということで無事AZIKを入れることができた。ATOKはなんか同期機能とかが嬉しいらしいので、AZIKにしていなかったMacBook ProのほうもAZIKにしようかな。辞書も共有できるらしく、それは普通にかなりありがたい。
-
少なくともAZIK考案者とGoogle日本語入力は「ローマ字テーブル」と呼んでいる。初見で意味が伝わりそうなのでこれに統一する↩
