QWERTY順にソートされた辞書
「たまにABC順に並んだキーボードってありますよね」というところから、「逆にQWERTY順に並んだ英語辞書を見てみたい」という話になった。
まずは考察
q の後には基本的に u が来るものである。しかも QWERTY 順で u はかなり最初の方にあるので、辞書の冒頭は que- で埋まるだろう。qwerty 自体も語としてあることを考えれば、q → qwerty → queer → queen といった配列になるだろうか。
検証
こういう書き捨ては JavaScript でいいだろうと考え、とりあえず比較関数を書く。Haskell とかで書いた方が楽だったかもしれないが、今使ってるマシンに Haskell が入ってないので愚直に書くことに。
var comp = (a, b) => { if (a === "") return -1; if (b === "") return 1; var af = "qwertyuiopasdfghjklzxcvbnm".indexOf(a[0]); var bf = "qwertyuiopasdfghjklzxcvbnm".indexOf(b[0]); if (af < bf){return -1;} else if(af>bf){return 1;} else return comp(a.slice(1), b.slice(1))}
あとは英単語の一覧を http://www-personal.umich.edu/~jlawler/wordlist.html から持ってきてやって、ソートすれば:

あー、そういえば QED があった。
辞書の終わりのほうはどんな感じだろうか。

なるほどなぁ。
誰かやって
- Webster's Dictionary, 1913 とかの版権の切れた辞書を使って、QWERTY順にソートし直しただけの辞書を作って刷ってほしい
紙と鉛筆しかないときに便利な暇つぶし
紙と鉛筆しかないときってありますよね。今日まさにそういう状況が発生したので、そういった際に私が行う様々な暇つぶしのうちの一つを紹介しようと思います
公式
$\frac{n!}{\left(\frac{n+x}{2}\right)!\left(\frac{n-x}{2}\right)!}\approx\frac{2^{n+1}}{\sqrt{2\pi n}}e^{-x^{2}/2n}$ という近似公式があります。*1 ということで、これを使って遊んでみましょうというのが今回のお題です。
n=6, x=2 のとき
左辺は $\frac{6!}{4!2!}=\frac{6\times5}{2}=15$。ということで、右辺に突っ込むことで、n とか x が小さいときにこの公式がどれくらいの精度で成り立つのかを確認したいわけです。
とりあえず $\frac{2^{7}}{\sqrt{6.28\cdot6}}e^{-4/12} \approx \frac{128}{6.14} e^{-1/3}$。えーっと $e^{-1/3}$ ってどうやって求めよう。あ、$e^{-1} \approx 0.367$ は覚えてる。つまり $0.7^3 \approx 0.343$ よりちょっと多い。よって $(0.7+x)^3 \approx 0.343 + 3\cdot 0.49 x$ を解きたい。引き算して $3\cdot 0.49 x = 0.024$。3で割って2を掛けると $x = 0.016$ といったところか。ということで $e^{-1/3} \approx 0.716$ が無事求まった。
$\sqrt{6.28\cdot6} \approx 6.14$ だから、結局 $\frac{128}{6.14} \times 0.716$ だから、えーと $128 \times 716$ を真面目に筆算して、$\frac{91.6}{6.14} = \frac{1}{2}\times\frac{91.6}{3.07}$。はいはいだいたい15っぽいですね。オーケー。
n=100, x=4 のとき
右辺は $\frac{2^{101}}{\sqrt{6.283\cdot100}}e^{-\frac{16}{200}}$ 。えー $e^{-0.08} = 1 - 0.08 + 0.0032 = 1-0.00768$ としてやればよい。2の常用対数は $0.3010299$ とかのはずなので、101倍してやって $2^{101} \approx 10^{30.404}$。平方根はだいたい$\sqrt{625} = 25$ ……だとちょっと精度が足らん気がするな。精度というのは稼げるところで稼いでおきたいので、もうちょい頑張っておくか。えっと $\sqrt{625 + 3.3} = 25\sqrt{1+\frac{3.3}{625}} = 25\sqrt{1+\frac{52.8}{10000}}$ だから、全体に $1-0.00528$ を掛けてやればいい。(※計算ミス!平方根の中から取りだしたのだから、本当は半分にしてやらなきゃいけない。あとそもそもここまでの精度要らない)
ということで求めるべきは $\frac{10^{30.404}}{25}\left(1-0.00528\right)\left(1-0.0768\right)$ であって、100を25で割ってやって $4\cdot 10^{28.404} \cdot \left(1-0.0821\right)$。
さて残るは $10^{0.404}$ の処理だけども……あ、$10^{0.404} \approx \left(10^{0.301}\right)^{4/3}$ としてやれば、これはオクターブと長三度。完八が2/1、完五が3/2、完四が4/3、長三が5/4、短三が6/5なのだから、$2^{1/3} \approx 1.25$。
……真の値はもうちょい大きかった気がする。まあたしかに $125/64 < 2$ だもんな。じゃあ $1.26$ にしておくか。ということで $4\cdot2.52\cdot(1-0.0821)\cdot 10^{28} \approx 9.26\times 10^{28}$ かな。
答え合わせ
- $\frac{2^{7}}{\sqrt{6.28\cdot6}}e^{-4/12} \approx 14.94$
- $\frac{100!}{48!52!} \approx 9.32\times10^{28}$
- $\frac{2^{101}}{\sqrt{6.28\cdot100}}e^{-\frac{16}{200}} \approx 9.34 \times 10^{28}$
ということで、だいぶいい線いけた。
実際の計算用紙

入力に5打必要なハングル
きっかけ
KMC(京大マイコンクラブ)に入って2ヶ月が経とうとしていた今日この頃、例会があったので(こちらは午前3時であるにも関わらず)参加した。例会が終わった後、することもないので(いや寝ろよ)韓国語の単語帳を回していたところ、pelkさんという方から「常々思ってたんですけどハングルってキーボードでどう入力するんでしょう」という質問を頂いた。
その質問に対して、私は「ハングルの入力は、まあある種のIMEを使うのが普通です。ㅇㅏㄴㅎㄷㅏと入力すると、順にㅇ→아→안→않→않ㄷ→않다となります」とテキストチャットで書いたあとで、Google Docs を開き、韓国語作文を即興でしながら入力する様子を画面共有をすることで、実際の入力の様子を見せて説明することができた。
ほえ~
パーツごとに入力していくのか
最大で4パーツ組み合わさりえて, 該当する文字が無ければ即座に次の文字に入力されるんだなぁ
とテキストチャットに書かれているのを見つけた私は、「あ、ㅚとかの一部の母音字は入力に2打を必要とするので、(まあこんな音節はないんですが)욊という音節を入力するには5打必要になりますね」とコメントした。
さて、韓国語初学者である私はここでサクッと5打必要となる音節の実例を提示することができず、入力はできるけれど実際には用いられない文字を使って説明をしてしまったわけだ。ということで気になるのが、果たして実際に使う単語でこの条件を満たす具体例があるのかということである。調べてみよう。
KS X 1001
韓国語がそんなにできないにも関わらず「実際に用いられる文字」の一覧を持ってくるにはどうすればいいか。そういうときに役に立つのが、韓国語のレガシーエンコーディングである KS X 1001 というやつである。このエンコーディングは、韓国語で実際に使う音節のうち、頻度の高い 2350 字を収録している。(ただし、出現頻度がある程度低いやつは入っていないので、例えば하얬다「白かった」に出てくる얬という字が収録から漏れていたりする)
出現頻度とかで決めたからあんまり出ないやつは入ってなかった。これで하얬다が書けなくて困った思い出。
— 広島鍋 (@hiroshima_pot) 2021年1月30日
また、この選出は1987年に行われたので、翌年の正書法改訂で消えた뭏という字(아뭏든「とにかく、いずれにせよ」。今は아무튼と書く) が入っているといった細かい話もある。まあそれはそれとして、とりあえずサクッと使えるのでこの中から探すことにする。
探し方
今回探し求めているのは、以下の条件を満たすやつである。
- 母音字として ㅘ, ㅙ, ㅚ, ㅝ, ㅞ, ㅟ, ㅢ のどれかを含む
- 終声として二重パッチム ㄳ, ㄵ, ㄶ, ㄺ, ㄻ, ㄼ, ㄽ, ㄾ, ㄿ, ㅀ, ㅄ のどれかを含む
今私が使ってるWindows標準のやつだと、2打連続で同じ子音字を打つことによって濃音を入力することはできず、Shift を用いた入力しか受け付けないので、そのような入力は今回は考えないことにした(というか、濃音パッチムがアリなら됐(~になった)即座に提示していた。さすがに됐がパッと出るくらいの韓国語力は私にもある)。同様に、ㅐやㅔは一打での入力しかできないので、これらもカウントしない。
さて、どうやって探すかだが、こういう書き捨ての探索はブラウザの JavaScript コンソールでやってしまうのが手っ取り早い。便利なことに、Namuwiki の완성형/한글 목록/KS X 1001(訳すと、「完成形/ハングル目録/KS X 1001」)というページにスペース区切りで一覧が入っているので、
var a = "가 각 간 (中略) 힘 힙 힛 힝".split(" ")
としてやれば配列aにハングル一覧が入る。さて、この中から
- 母音字として ㅘ, ㅙ, ㅚ, ㅝ, ㅞ, ㅟ, ㅢ のどれかを含む
- 終声として二重パッチム ㄳ, ㄵ, ㄶ, ㄺ, ㄻ, ㄼ, ㄽ, ㄾ, ㄿ, ㅀ, ㅄ のどれかを含む
という条件を満たすやつを探してやらなければならない。これをするには、Unicodeで定義されている NFD というやつを使うのが便利である。例えば、값 (U+AC12, HANGUL SYLLABLE GABS) という字をNFDに突っ込むと、以下のように3つに分解される。

こう分解されてしまえばもうこっちのもので、後はこれらが条件を満たすかどうかを探るだけでいい。とりあえず、NFDしたやつの n 番目を抜き出す関数を定義して、
var f = (str,n) => str.normalize("NFD")[n]
母音に関する条件を記述して、
var vowel_condition = (s) => [..."와왜외워웨위의"].map(c => f(c, 1)).includes(f(s, 1))
子音についても書いて、
var consonant_condition = (s) => [..."갃갅갆갉갊갋갌갍갎갏값"].map(c => f(c, 2)).includes(f(s, 2))
フィルターを掛けると……

なんと、「괆」ただ一字だけが条件を満たすことが判明!!!!
この形はだいたいㄹ語幹の動詞を名詞化したものなので、괄다で調べると……ありました、「火の勢いが強い」「せっかちで荒々しい」「(生地などが)ごわごわしている」「(木の)やにが多い」。うん、どう考えても初学者が知らない単語です。
結論
- KS X 1001 に出てくる字の中で唯一5打を必要とする特別な文字「괆」。「火の勢いが強いこと」「せっかちで荒々しいこと」「(生地などが)ごわごわしていること」「(木の)やにが多いこと」という意味を表すことができる文字です。
- こいつをクビにして「白かった」とかを入れた方がよかったんじゃなかろうか、KS X 1001。
語学と私 (part3) ― IDIEZという(比較的思想の強い)団体が提供するナワトル語教育を3学期間受けた感想 ―
part 1 はこちら。
part 2 はこちら。
前回までで、ナワトル語の授業を履修することにしたきっかけについては記述したので、以降はその授業がどんな感じであり、履修してどうであったかについて書く。
「ナワトル語」の授業
前回言及した
人「なにやってるんですか」
私「ナワトル語の単語帳回してます」
人「ナワトル語ってなんですか」
私「アステカ帝国の公用語で、今でも160万人ぐらいが話してるみたいですね」
人「はえー」
についてだが、これは実際の構図を(意図的に)ちょっと単純化しすぎた表現になっている。
まず、「アステカ帝国の公用語」というのは(大雑把に言うと)話題が16世紀であり、一方で「今でも160万人ぐらいが話してる」という話題は当然21世紀の話である。前回言及した Launey, M., & Mackay, C. S. (2011). An introduction to classical Nahuatl. New York: Cambridge University Press. の Preface を引用するなら、
Let us specify again that the language described here is Classical Nahuatl, the literary language of the century following the Conquest. Nearly five centuries on, there is clearly no region in which this variety of Nahuatl is still spoken. It is thus a dead language, or rather, a dead variant of a language, in the same way as the English of, say, Christopher Marlowe is a dead form of the English language. No one nowadays speaks exactly like that, but many hundreds of thousands of people speak present-day variants of Nahuatl, some of them fairly close to the classical one, so that travelers to Mexico today may be pleasantly surprised when recognizing words and expressions, thereby gaining more inside knowledge of the country and its people.
「Christopher Marlowe の話していた英語」と言われても伝わらないと思うので、日本語で同じあたりの年代の例を探すなら、1592年の天草版『平家物語』の表紙にある、
NIFONNO
COTOBA TO
Hiſtoria uo narai xiran to
FOSSVRV FITO NO TAME-
NI XEVA NI YAVA RAGVETA-
RV FEIQE NO MONOGATARI.
「日本(にふぉん)の言葉とイストリアを習い知らんと欲(ふぉっ)する人(ふぃと)のために世話(しぇわ)にやわらげたる平家(ふぇいけ)の物語」
とかを提示するのが無難なのかもしれない(歴史の教科書で見たことがあるという人もいるだろうし)。

ということで、なにが言いたかったかというと、前述の通り
であるがゆえに当然この両者の間に差があるぞ、ということである。
さて、今回私が受けたのがナワトル語の授業である旨は散々述べてきたが、これは古典ナワトル語の授業ではない。21世紀に話されている言語を、その言語の母語話者から習ったのである。
IDIEZという団体
今回受けた授業を主催していたのは、IDIEZという団体である。サイトは
http://www.idiezmacehualli.org/ 。まずトップページを見ると、
IDIEZ A.C., es una asociación civil sin fines de lucro, promueve la investigación, la enseñanza y la revitalización de la lengua náhuatl
ナワトル語の研究・教育・言語復興をする団体と書いてある。さて、
El curso que ofrece IDIEZ se enfoca en la cultura y lengua náhuatl (variante de la Huasteca Veracruzana) con un desarrollo curricular de cuatro niveles.
ナワトルの文化と言語(ワステカ・ベラクルス方言)に焦点を当てるとしている。ということで、ナワトル語の中でも「現代ワステカナワトル語」 の授業である、という断り書きを入れておいた方がいいだろう。(cf. Huasteca Nahuatl - Wikipedia) ワステカナワトル以外にも様々な現代ナワトルがあるということにも注意されたい。
ワステカ方言は現代語の最大方言なので、サカテカス組とワルシャワ組が組んで、チコンテペクというワステカ方言の村をベースにして盛んに出版とかやってるんですよね。マヤ系のワステコとは別です。
— Mitchara (@Mitchara) 2019年2月22日
英語版Wikipediaによると、この方言差はそこそこ大きいので相互理解ができるほどではないと書いてある。一方IDIEZ側は「現代ワステカナワトル語を学べば他の方言も分かるようになるよ」と主張していた。この主張はどちらかというとプロパガンダ寄りに私には見えた。他の現代ナワトル語を記述した研究書とかも読んでみたが、やはり現代ワステカナワトル語だけの知識では全然わからないところもかなりある。もちろん分かるところもたくさんあるが。
正書法規則
IDIEZ は古典ナワトル語のアルファベット表記*1にめちゃめちゃ寄せて現代ワステカナワトル語を書く。古典ナワトル語のアルファベット表記というのは、スペイン語を話す人々が作ったものであるので、当然ながら当時のスペイン語に基づいた表記になっている。
さて、当時のスペイン語は k というアルファベットを使わなかった(今でも外来語ぐらいにしか使わない)。ということで「カ」という音を書くには ca と書き、「コ」という音を書くには co と書く。さて、「キ」はどう書くか。ci と書きたくなるが、なんとスペイン語ではこれは「スィ」と読む。ということで「キ」は qui と書き、同様に「ケ」は que と書く。
逆に、「スィ」「セ」は ci, ce と書くが、「サ」「ソ」は ca, co と書くわけにはいかないので za, zo と書く。
結果として、
| ca カ |
qui キ |
-c -ク |
que ケ |
co コ |
| za サ |
ci スィ |
-z -ス |
ce セ |
zo ソ |
という体系になる。なお、この体系は現在のスペイン語でもバリバリ健在である。たとえば amar (アマル)「愛する」から「私が愛した」を作るには -ar (アル) を取り -é (エ) を加えて amé (アメ)とするのだが、practicar (プラクティカル)「実行する・練習する」から「私が実行した・練習した」を作るには、同じく「アル」を取り「エ」を加えるので「プラクティケ」となる。しかし「ケ」は que と書くので、 practicar が practiqué になるという綴り字の上での変化を喰らう。同様に、「始める」は comenzar (コメンサル)なので「私が始めた」は当然「コメンセ」であるが、これも comenzé ではなく comencé と綴るので、 comenzar が comencé になるわけである。
また、当時のスペイン語は w というアルファベットを使わなかった(今でもやっぱり外来語ぐらいにしか使わない)。ということで*2、ナワトル語にもあるクヮ行やワ行は以下のように表記する。
| cua クヮ |
cui クィ |
-uc -クゥ |
cue クェ |
| hua ワ |
hui ウィ |
-uh -ゥ |
hue ウェ |
あと、当時のスペイン語では x はシャ行のような音であった *3 ので、ナワトル語のシャ行も x で綴る。たとえば México という国名自体がナワトル語 Mēxihco (メーシッコ) を書き写したものである。ただ、スペイン語の方ではその後シャ行の音がハ行に変化したので、現在のスペイン語では México は「メヒコ」と読む。
話が逸れるが(ほらこうやってどんどん記事が長くなる)、スペイン語をご存知の方のためにさらに補足。日本でスペイン語を学ぶと、z だったり ci, ce だったりは英語の th の音として教わると思うが、当時は ci, ce とかは「スィ」「セ」に近い音で、sa, si, su, se, so は(x- とはまた微妙に異なる)シャ行っぽい音であったとされている。詳しいことは https://en.wikipedia.org/wiki/Early_Modern_Spanish と
https://en.wikipedia.org/wiki/Nahuatl_orthography と
https://en.wikipedia.org/wiki/Phonological_history_of_Spanish_coronal_fricatives をご覧頂きたいが、せっかくなのでナワトル語に絡んだ話をしておくと、たとえばスペイン語 Castilla「スペイン、カスティーリャ」(カステラの語源でもある。もちろんカステラの方はポルトガル語を経由しているが)は古典ナワトル語では Caxtillān という形で入っているし、逆にナワトルの xōchitl (ショーチトル)を suchitl と s で表記している写本もあるようである。他の例は https://davidbowles.medium.com/mexican-x-part-xi-rise-of-a-new-x-4c30c0f74ad8 など。
まだ延ばすのかよ
さて、前回タイトルに 「IDIEZという(比較的思想の強い)団体が提供するナワトル語教育を2学期間受けた感想」と入れることができなかったので今回は「IDIEZという(比較的思想の強い)団体が提供するナワトル語教育を3学期間受けた感想」をタイトルに入れてみたが*4、感想もほぼ書いていないし IDIEZ の思想の強さにも全然言及できていない。ということでこの連載はもうちょい続く予定である。
*1:普段の私なら「ラテン文字表記」とか書いちゃうけど、これは一応一般向け記事ということになっているので
*2:この書き方には語弊がある。たとえば、当時のスペイン語ではクヮという音は qua と書いたりしたので、Launey, M., & Mackay, C. S. (2011). An introduction to classical Nahuatl. New York: Cambridge University Press. によると、実際の写本ではクヮは qua と書かれることが多かったらしい。というか1815年まではスペイン語では cuando とか cuatro とかは quando や quatro と綴るのを正則としていたようである。ワ行については、そもそも hu- で綴るのは珍しく、ワ・ウィ・ウェはそれぞれ ua/oa, ui/vi, ue/ve と綴るのが普通だったとのことである。
*4:学期の数が1個増えていることに注意。もたもたしてたら記事を書き上げる前に春学期終わっちゃったよ
理想的な弦ではなく、理想的な長い板を叩いたときの周波数比に由来する「12.3音平均律」
概要
12音平均律というのは、理想的な弦の振動による周波数比が 1 : 2 : 3 : 4 : 5 : 6 : ... となることと、$2^{7/12} = 1.4983\dots \approx \frac{3}{2}$ および $2^{4/12} = 1.2599\dots \approx \frac{5}{4}$ であることに由来する。完全八度を12分割して得られる代物を共通尺度にすることで、そいつを7つ集めて純正完全五度っぽいものが、そいつを4つ集めて純正長三度っぽいものが再現できてうれしい、というのが12音平均律の根拠である。
さて、では「理想的な弦の振動」ではなくて「理想的な長い板の振動」ならどうであろうか。あ、今回は自由端だけ扱うこととする。
結論を先に言うと、周波数比は 3.0112² : 4.9995² : 7² : 9² : ... になる。この周波数比に言及している文献はわりとあったが、導出してるやつがなかなか見つからずに私が苦労したのでまずはこれの導出をしてから、「12.3音平均律」の提唱に移りたい。
周波数比の導出
微分方程式
オイラー・ベルヌーイの梁理論というやつを使うと、長さ $L$ の梁が材料においても断面の形においても一様である場合、たわみ $w(x, t)$ ($x$ は梁の伸びている方向に沿って定義された座標)の挙動を表す微分方程式は
$$EI\frac{\partial^4 w}{\partial x^4} = \left(- \frac{\partial^2 w}{\partial t^2} \right)\rho A$$
と書ける。ここで $\rho$ [kg/m³] は素材の密度、$A$ [m²] は梁の断面積。$EI$ [N・m²] は曲げ剛性と言われる量であり、材質により決まる弾性率 $E$ [Pa] と、断面の形によって決まる量である面積の第二モーメント $I$ [m⁴] を掛け合わせたものであるらしい。重力加速度は無視したが、欲しい場合はカッコでくくった $- \frac{\partial^2 w}{\partial t^2} $ の項にさらに重力加速度を足せばいい。
境界条件
さて、二階微分というのは曲線が局所的にどれくらい強く曲がっているかを表すわけで、たわみの $x$ についての二階微分 $\frac{\partial^2 w}{\partial x^2}$ は両端 $x=0$ と $x=L$ でゼロになる。
自由端なので、両端での剪断応力もゼロになる。したがってたわみの $x$ についての三階微分も両端でゼロである。
方程式を解く
$$\left(EI\frac{\partial^4 }{\partial x^4} + \rho A \frac{\partial^2 }{\partial t^2}\right) w = 0$$
を解くために、まず $w(x,t) = X(x)T(t)$ という形の解を仮定して
$$\frac{EI}{\rho A} \frac{1}{X}\frac{d^4 X}{d x^4} = - \frac{1}{T}\frac{d^2 T}{d t^2}$$
どうせ $T$ は角振動数 $\omega$ の三角関数で、したがって $\frac{EI}{\rho A} \frac{1}{X}\frac{d^4 X}{d x^4} = \omega^2$ となればよい。 $k = \left(\frac{\rho A \omega^2}{EI}\right)^{1/4}$ と置いて $\frac{d^4 X}{d x^4} = k^4X$ と書いてやれば、
$$X = \alpha \mathrm{cos h}(kx) + \beta \mathrm{sin h}(kx) + \gamma \cos(kx) + \delta \sin(kx)$$
になることがすぐにわかる。さて境界条件。
$X'' = k^2 (\alpha \mathrm{cos h}(kx) + \beta \mathrm{sin h}(kx) - \gamma \cos(kx) - \delta \sin(kx))$ と $X''' = k^3 (\alpha \mathrm{sin h}(kx) + \beta \mathrm{cos h}(kx) + \gamma \sin(kx) - \delta \cos(kx))$ が $x=0$ と $x=L$ の両端でゼロになる必要があるので、
$$\begin{pmatrix}1 & 0 & -1 & 0 \\ \mathrm{cos h} kL & \mathrm{sin h} kL & -\cos kL & -\sin kL \\ 0 & 1 & 0 & -1 \\ \mathrm{sin h} kL & \mathrm{cos h} kL & \sin kL & -\cos kL \end{pmatrix} \begin{pmatrix}\alpha \\ \beta \\ \gamma \\ \delta \end{pmatrix} = \begin{pmatrix}0 \\ 0 \\ 0 \\ 0\end{pmatrix}$$
第一行と第三行(つまり $x=0$ での境界条件)を見ると $\alpha = \gamma$ と $\beta = \delta$ が分かるので、
$$\begin{pmatrix} \mathrm{cos h} kL -\cos kL& \mathrm{sin h} kL -\sin kL \\ \mathrm{sin h} kL + \sin kL & \mathrm{cos h} kL - \cos kL \end{pmatrix}\begin{pmatrix}\alpha \\ \beta \end{pmatrix} = \begin{pmatrix}0 \\ 0 \end{pmatrix}$$
ここで
$$\begin{align*} \det \begin{pmatrix} \mathrm{cos h} kL -\cos kL& \mathrm{sin h} kL -\sin kL \\ \mathrm{sin h} kL + \sin kL & \mathrm{cos h} kL - \cos kL \end{pmatrix} &= ( \mathrm{cos h} kL -\cos kL )^2 - (\mathrm{sin h} kL - \sin kL)(\mathrm{sin h} kL + \sin kL)\\
&= \cos^2 kL - 2\cos kL \mathrm{cos h} kL + \mathrm{cos h}^2 kL - \mathrm{sin h}^2 kL + \sin^2 kL \\
&= 2 - 2\cos kL \mathrm{cos h} kL\end{align*}$$
であることに着目すると、$\cos kL \ \mathrm{cos h} kL - 1 = 0$ でない限り先ほどの方程式に非自明解が存在するはずがない。
これをプロットしてみると、
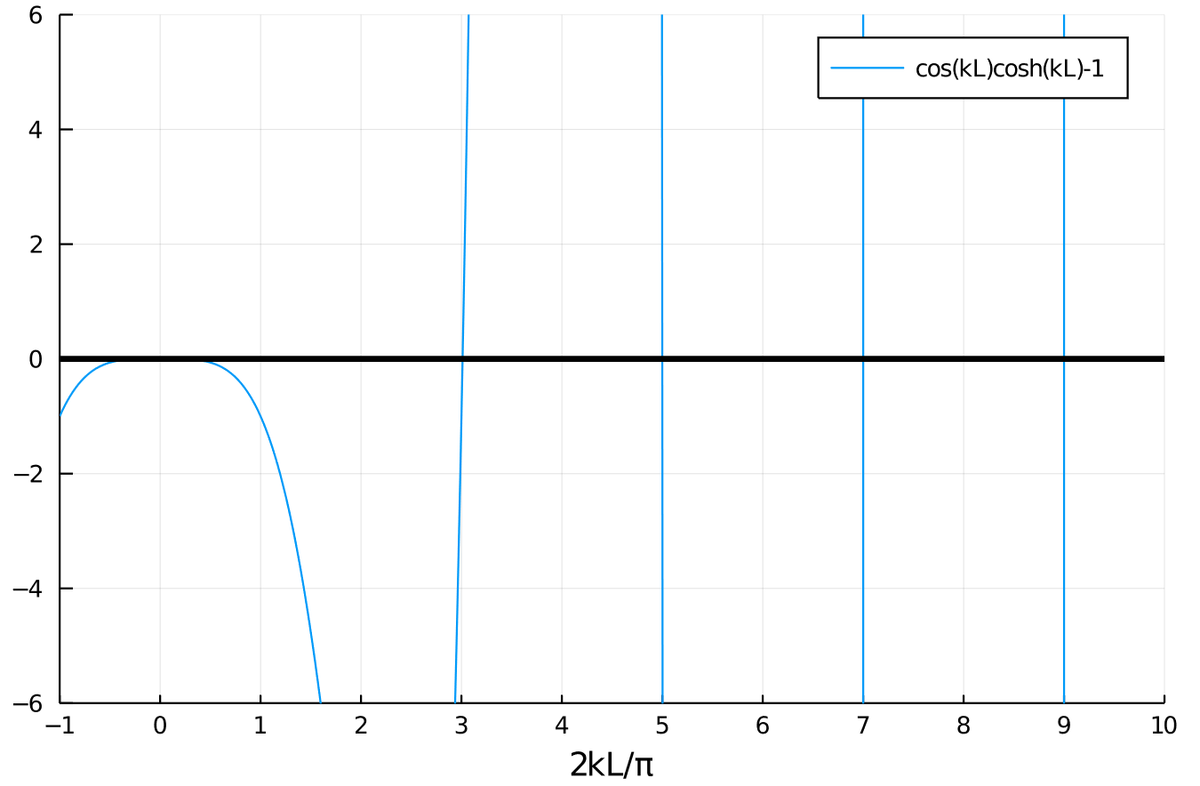
お、3 : 5 : 7 : 9 の謎が見えてきた。
近似
ということで、 $\frac{2kL}{\pi}$ は $3, 5, 7, \dots$ にかなり近いっぽいので、これを評価するために $a_n$ を$1 = \cos(\pi a/2)\ \mathrm{cos h}(\pi a/2)$ の $n$番目の正の解とすると、グラフから $\epsilon_n = a_n - (2n+1)$ が非常に小さい値であることが見て取れる。具体的にどれくらい小さいかを調べるために元の式に代入し直すと、
$$\begin{align*}1 &= \cos\left(\frac{\pi}{2} (2n + 1 + \epsilon_n)\right) \cdot \mathrm{cos h}\left(\frac{\pi}{2} (2n + 1 + \epsilon_n)\right) \\1&\approx -(-1)^{n}\frac{\pi \epsilon_n}{2}\cdot \frac{1}{2} \exp\left(\frac{\pi}{2} (2n + 1)\right)\end{align*}$$
ということで
$$ \epsilon_n \approx -(-1)^{n}\frac{4e^{-\pi / 2}}{\pi } \exp\left(-n\pi \right) $$
と近似できる。右辺に $n=1$ を代入したときの値は $0.01143788\dots$ であり、前述の $3.0112$ をちゃんと説明できる。
周波数比に共通尺度を入れる(弦について)
12音平均律というのは $\ln 2, \ln 3, \ln 5$ をそれぞれ $12 \cdot \frac{\ln 2}{12}, 19 \cdot \frac{\ln 2}{12}, 28 \cdot \frac{\ln 2}{12}$ として近似して得られるのであった。つまり、$\ln 2$ の長さの棒・$\ln 3$ の長さの棒・$\ln 5$ の長さの棒が手元にあるとき、$\ln 2$ を12等分して得られた棒を整数本使うと、わりと精度良く $\ln 3$ や $\ln 5$ を測ることができる、ということである。
さて、この「12等分が比較的いい感じの結果を与える」というのはどのように定量化してやればよいのだろうか。一般に、長さ $1, b_1, b_2$ の棒があったときに、「長さ $1$ の棒を $ n $ 等分して共通尺度として用いることは、 $ m $ 等分して共通尺度として用いることよりも適切である」というのはどうやって定式化すべきだろうか。
直観的には、「$nb_1$ と $nb_2$ はともに整数に近くて、$ mb_1 $ と $ mb_2 $ はそれほど整数に近くない」ということを表現したい。ということで、二乗誤差を足し合わせた $ \sum_{i} (n b_i - \operatorname{round}(n b_i))^2 $ を小さくすることを考えてみる。これを「相対誤差」とでも呼ぶなら、これを $n^2$ で割ったものは「絶対誤差」と呼べるだろう。
1 : 2 : 3 : 4 : 5 の周波数比について、実際にプロットしてみるとこの通り。
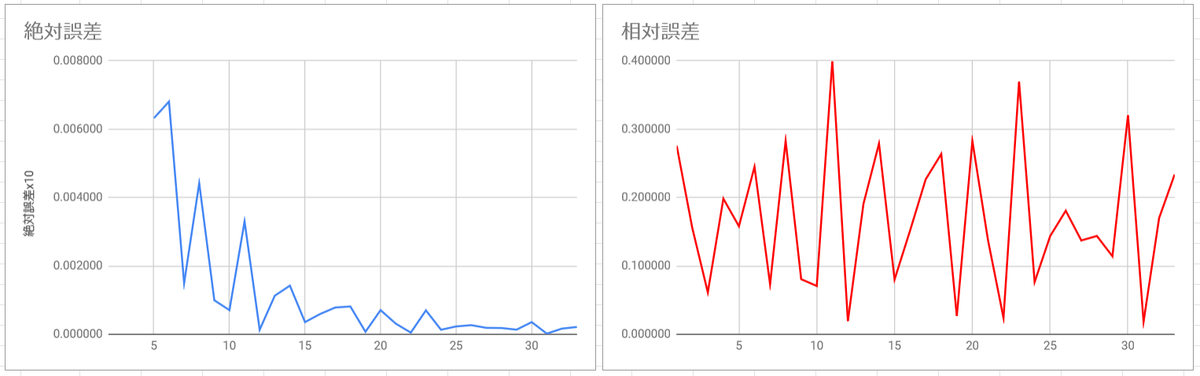
「良い」とされている12分割・19分割・22分割・31分割がこの評価方法で明確な谷として現れることは、この評価方法がわりと有効であることを示唆する。
周波数比に共通尺度を入れる(長い板について)
さて、評価方法が決まったので、さっそく長い板の周波数比についてもやってみよう。
a₁² : a₂² : a₃² : a₄² : a₅² ≒ 3.0112² : 4.9995² : 7² : 9² : 11² の周波数比について、実際にプロットしてみると、
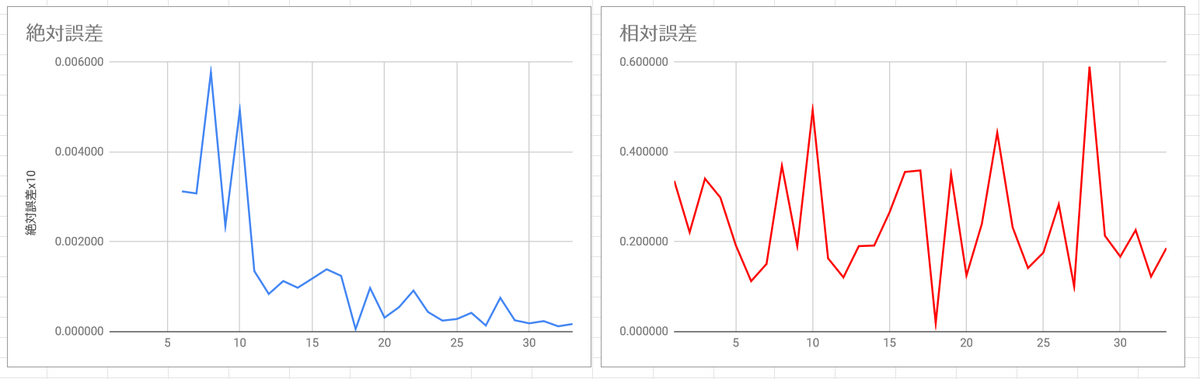
とまあ、18分割だけが突出してものすごく良いということが判明する。この共通尺度 $\left(\frac{a_2^2}{a_1^2}\right)^{1/18} = 1.0579\dots$ はセントに直すと$97.52$セントで、まあ12音平均律の半音よりちょっと狭いかなとなる。1200セントを$97.52$セントで割ると12.3なので、「12.3音平均律」みたいな呼び方をするとウケがいいのかもしれない。
語学と私 (part2)
おことわり
↑ の続編です。読んでない人は先に読んでおくことをおすすめします。
本文
ということで久々に語学というものを真面目にやりました。私という人間は根が不真面目でございますので、「語学を真面目にやる」というのは「真面目にやらないと不利益がそこそこ発生する環境に、置かなくてもいいのに自らを置く」とだいたい同義です。結果としてどうなったかはまあ察せている方もいるかと思いますが、「真面目にやらないと不利益がちょっと発生する環境に、置かなくてもいいのに自らを置いたが、やっぱり真面目にはやらなかったので不利益がちょっと発生した」というオチになるわけです。
じゃあナワトル語の授業を履修したことを後悔しているかというと、もう全くもってそんなことはありません。もともと私は後悔というものをする頻度が極端に低い人間ではありますがそれとは関係なく、むしろ「ナワトル語の授業を日本にいながら受ける」という非常に珍しい体験をすることができたというだけでもスタンフォード大学に所属した甲斐があったとまで感じています。
ナワトル語について
そもそも「ナワトル語」と聞いてピンとくる方ばかりではない(というか、どう考えてもピンと来ない方ばかりである)(と思ったがわざわざこんなタイトルのブログを読む人なら知ってるのが普通かもしれない)(とも思うがまあ一応書いておこう)と思うので概略だけでも。
ナワトル語の授業を受けている旨を口頭(こんなご時世なのでほとんどが Discord か VRChat、たまに Zoom)で言及する際に、テンプレ会話パターンとして使っていたのは以下の通り。
単語帳を回す私「ニクネキ・シキーシマティ・セー・ノテキシポホ。」*1
人「なにやってるんですか」
私「ナワトル語の単語帳回してます」
人「ナワトル語ってなんですか」
私「アステカ帝国の公用語*2で、今でも160万人ぐらいが話してるみたいですね」
人「はえー」
まあ雑談であまり長々と語ってもしょうがないわけで、これぐらいの簡潔さでまとめて話すことになるわけですね。アステカ帝国って単語はなんだかんだ皆さんご存知なのできれいにまとまる。
さて、ブログというのは対話とは違って私が一方的に長々と語る場なので、もうちょい書くことにしましょう。
まず、皆さん「アステカ」と「マヤ」の違いって分かります?そんなあなたにおすすめなのが ↓ の動画。(私はこの動画見るまで全然区別ついてませんでした。)「英語動画見るのつらい」って人は冒頭の20秒だけでも見といてください。
ナワトル語はこの「アステカ」の方です。
ナワトル語と私
ナワトル語について最初に目にしたのは、多分「ナワトル語には tl として綴られる音があって、こいつがおもしろい」みたいな話が日本語版 Wikipedia に書いてあったのを見たときな気がします(聞いてみたい方は、 tlahtlaniliztli. | Nahuatl Dictionary とかの音声を聞いてみるといいと思います)。
なお、実際にこれを発音してみたい方は、
- まず『タ』を言おうとし、寸止めする
- すると舌が口の上部(上の前歯の周辺)にくっつく。
- さて、普通『タ』を言うときは、このあと「下顎が下がることによって口が開き、舌もそれについていって口の下部に行く」という動きをするはずである(それを意識したことはないかもしれないが)。
- しかしながら、今回は舌の先端を意地でも上前歯から外さずに息を吐こうとしてみる。そうやって一瞬息が吐けたら、そのあとは意地を張るのをやめ、普通に『タ』を言うときの挙動をしてみる
をやると、だいぶいい感じの tla が言えると思います。*3
その次に目にしたのは多分国際言語学オリンピック2015(ブルガリア大会)に出場したときのことで、 ナワトル語の数詞体系に関する問題とかをブルガリアに行って解きました。(問題文はここにあります。)(あ、上記問題をネタバレ無しで解いてみたいという方は、このブログを読み進める前に解いておいてください。後でネタバレ書きますので。)
それから数年が過ぎ、私はTwitterを始め、2017年12月にはこんなツイートをRTしていたようです。
古典ナワトル語、まず挨拶するために敬語活用に必要な充当形と使役形を覚えて、そのために動詞の価数と再帰形と初級の難関である3群動詞の語幹交替をマスターしないと、人に会って挨拶もできないあたりが、語学としての不人気の理由なのかもな #これでもナワトル語はメソアメリカで一番簡単な言語です
— Mitchara (@Mitchara) 2017年12月5日
さらに数年が経ったある日(具体的には2019年8月18日)のこと。
国際先住民語年、そういえば今年はコルテスのメキシコ上陸500周年だからだろうか。それについてはまあ昨日今日先住民語を始めたわけではないので何も言うことはありません。ありませんが、ナワトル語はわずか5000円で習得できるということは申し上げておきます https://t.co/jS9lRbn0Aa
— Mitchara (@Mitchara) 2019年8月18日
というツイートが流れてきて、さっそく Launey, M., & Mackay, C. S. (2011). An introduction to classical Nahuatl. New York: Cambridge University Press. の Kindle版を買いました。
かなしいことに、Kindle版は組版がつらいことになっており、読むに耐えませんでした。
これKindleで買ったらマクロンが画像で入っててめちゃめちゃ読みにくかったので、みなさん紙で買いましょう https://t.co/LhY9S9lg2G
— jekto.vatimeliju@hsjoihs@.sozysozbot. (@sosoBOTpi) 2019年10月5日
ということで、 2019年10月には紙版も購入。
それと並行して、創作自然言語などを行う集まりがスタンフォード大学に存在することを知り、参加。 *4
なんかこういうものがあるらしいので顔を出してみようかと pic.twitter.com/GrnuZkqdyt
— jekto.vatimeliju@hsjoihs@.sozysozbot. (@sosoBOTpi) 2019年10月24日
すると、まあやはり言語の話で盛り上がるわけでして。
早速ラテン語とナワトル語とクウェンヤの話が始まった
— jekto.vatimeliju@hsjoihs@.sozysozbot. (@sosoBOTpi) 2019年10月24日
この回だったかそれ以降の回だったかは覚えていませんが、手元にあった言語周りの本を全部(当然ナワトル語の文法書を含む)カバンに詰めて持参したりして場を盛り上げたりもしたはずです(「あれ、受身ってどう表現するの?」みたいな質問にその場で開いて答えることができてたのしかったです)。
さて、その後の何らかのタイミングで文法書の全ページを眺める作業(この行為に「読む」という動詞を用いていないことに注意。つまり眺めただけで読了後になんも覚えていない様を表す。)を行ったことは記憶にあるのですが、いつだったのかを一切覚えていません。2020年3月からロックダウンして、2020年6月に日本にこっそり帰ってきたのは確実だけれど、読了は日本に帰ってきてからだったかなぁ~?んー、自信がないです。
それはともかく、文法書の全ページを眺める作業を行った以上、せっかくナワトル語が開講されているならそれを履修するしかないわなということで、
前回 ↑ 書いたように、ナワトル語の授業を取ることにしてみました。
前置きが長くなりすぎた
えーと、この記事はもともと「IDIEZという(比較的思想の強い)団体が提供するナワトル語教育を2学期間受けた感想」というタイトルにしようと思っていたんですが、IDIEZという語すら登場せず4000文字に達しようとしているので、一旦記事を分けます。
*1:「私の友達に会って欲しい」。興味のある方のために書いておくと、Nicnequi xiquīxmati cē notequixpoh. は nicnequi /nikneki/ (ニクネキ) 【ni-「私が」 + k-「彼・彼女・それを」+ neki「欲する」】、xiquīxmati /šikiːšmati/ (シキーシマティ) 【ši-「あなたが~しろ」 + k-「彼・彼女・それを」+ īšmati「~と会う」】、cē /seː/ (セー)「ひとつの」、notequixpoh /notekišpoh/ (ノテキシポホ) 【no-「私の」 + tekišpoh「友達」 】から構成される。
*2: lingua franca という表現は一般人に通じるわけないので
*3:「あれ? [t͡ɬ] ってそんな音なの?」と疑問に思った方のために、ツイートを一つ貼っておきます。
IPAというかその運用についていうと、なんでみんなナワトル語の tl 音を [tɬ] って書くの。IPAには [tˡ] の記号があるし、それ使えばナバホ語の tł / dl / tł' だってちゃんと書き分けられるんだから、普通にそれ使えばよくない? ねえ?
— Mitchara (@Mitchara) 2018年10月21日
*4:普通「人工言語」と呼ばれるタイプの創作活動。↓ に従い、ここでは「創作自然言語」表記を用いる。
ぼくが「創作自然言語」っていう単語を使うのは、ぼくは情報系の人間なので、「人工言語」っていうと先に「工学言語/プログラミング言語/etc.」を思い浮かべる方がTLに多いからなのですよね
— ゆーちき (@yuchiki1000yen) 2020年5月30日
ちょっと長ったらしいけど、まあ紛らわしさは減るかなと思って
ピタゴラスで √n な螺旋
概要
皆さんは、以下のような図形を見たことがあるだろうか。私はある。

如何なる機会にこれを見たのかはもはや定かではないが、たしか作図可能数の議論をする際に「自然数の平方根についてはこのように作図することができる」という例示としてなんらかの本で出てきていた気がする。直角を作図できるので直角三角形が作図でき、一辺の長さが1となるような直角三角形を積み重ねれば√nが作図できるということである。
この図のことは長らく忘れていたが、スーパーマリオ64 RTA/TAS用のWikiを今日なにげなく読んでいたところ、
この図のことを思い出した。ということで、ちょっとこいつについて考えてみる。
挙動
まず $f\left(k\right)=\sum_{n=1}^{k}\mathrm{a r ctan}\left(\frac{1}{\sqrt{n}}\right)$ を定義してやることにより、各頂点は極座標上で $(r, \theta) = (\sqrt{N}, f\left(N-1\right))$ と書ける($N=0$とすると原点もカバーされていてくれたりする)。ということで $f(k)$ を調べてやることで挙動がわかる。
とりあえず雑に見積もる。$\sum_{n=1}^{k}\mathrm{a r ctan}\left(\frac{1}{\sqrt{n}}\right)$ というのはだいたい$\sum_{n=1}^{k}\frac{1}{\sqrt{n}}$ である。こいつはだいたい $\int_{1}^{k}\frac{1}{\sqrt{x}}dx$ であり、つまり $2\sqrt{k}$ ぐらいの速度で成長しそうだ。つまり $N$ が大きいときには $(r, \theta) \approx (\sqrt{N}, 2\sqrt{N})$ みたいな感じであり、$r = \frac{\theta}{2}$ なアルキメデス螺旋に似た振る舞いをしてくれそうである。
詳しい挙動
$f(k)$ はだいたい $2\sqrt{k}$ であることがわかった。さて $\lim_{k \to \infty} \left(f(k) - 2\sqrt{k} \right)$ って存在するんだろうか。desmosで実験してみた限りでは、しそう。ということで計算したい。
えー arctan をテイラー展開してやる。ただし $f(k)$ の初項は展開したやつが絶対収束ではないので、それだけ除外してやると、
$$f\left(N\right)=\sum_{n=1}^{N}\mathrm{a r ctan}\left(\frac{1}{\sqrt{n}}\right) = \frac{\pi}{4} + \sum_{n=2}^{N}\mathrm{a r ctan}\left(\frac{1}{\sqrt{n}}\right) = \frac{\pi}{4} + \sum_{n=2}^{N}\sum_{l=0}^\infty \frac{(-1)^l \left(\frac{1}{\sqrt{n}}\right)^{1 + 2 l}}{1 + 2 l}$$
総和を入れ替えたやつは
$$ \frac{\pi}{4} +\sum_{l=0}^\infty \frac{(-1)^l}{1 + 2 l} \sum_{n=2}^{N}n^{-l - 1/2}$$
ここで $l > 0$ の場合は $\sum_{n=2}^{N}n^{-l - 1/2}$ というのは $N \to \infty$ で $\zeta\left(l + \frac{1}{2}\right) - 1$ に収束する。$l = 0$ のときのはなんか Lampret, V. An accurate approximation of zeta-generalized-Euler-constant functions. centr.eur.j.math. 8, 488–499 (2010). https://doi.org/10.2478/s11533-010-0030-7 で the zeta-generalized-Euler-constant function という名前で呼ばれ、https://en.wikipedia.org/w/index.php?title=Euler%E2%80%93Mascheroni_constant&oldid=997546999 で Euler's generalized constantsと呼ばれている以下のやつ:
$$\gamma(s) = \lim_{n\to\infty}\left[\sum_{k=1}^{n} \left(\frac{1}{k^s} - \int_{k}^{k+1} \frac{dx}{x^s}\right)\right]$$
が使えそうである。結局 $\frac{\pi}{4}$ をバラさないと綺麗にならないので、絶対収束性を忘れて $\frac{\pi}{4}$ を解体することで、
$$f\left(N\right) - \int_{1}^{N+1} \frac{1}{\sqrt{x}}dx \to \gamma\left(\frac{1}{2}\right) + \sum_{l=1}^\infty \frac{(-1)^l}{1 + 2 l} \zeta\left(l + \frac{1}{2}\right) $$
$$f\left(N\right) - (2\sqrt{N+1}-2) \to \gamma\left(\frac{1}{2}\right) + \sum_{l=1}^\infty \frac{(-1)^l}{1 + 2 l} \zeta\left(l + \frac{1}{2}\right) $$
$$f\left(N\right) - 2\sqrt{N} \to -2 + \gamma\left(\frac{1}{2}\right) + \sum_{l=1}^\infty \frac{(-1)^l}{1 + 2 l} \zeta\left(l + \frac{1}{2}\right) $$
な気になれる。
うーん、なんも綺麗にならん!w